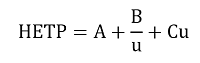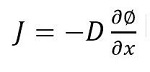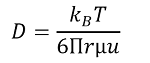前言
線速度是色譜學(xué)當(dāng)中一個(gè)重要的方法參數(shù)��,受流速、溫度����、色譜柱尺寸、流動(dòng)相類型等因素的影響����。在系統(tǒng)間轉(zhuǎn)移或重現(xiàn)色譜方法時(shí),線速度是需要重點(diǎn)考慮的因素之一����。它也可以用來調(diào)整運(yùn)行時(shí)間和/或改變色譜分離����,所以理解線速度的影響在方法開發(fā)和故障排查過程中很重要�。
一��、VanDeemter方程
提到色譜學(xué)當(dāng)中的線速度����,就不得不說起VanDeemter方程����。該方程是綜合考慮了分離過程中引起峰展寬的物理因素����、動(dòng)力學(xué)因素和熱力學(xué)因素后得到的單位柱長(zhǎng)的總峰展寬與流動(dòng)相流速的關(guān)系式�。其具體表達(dá)式如下[1]:
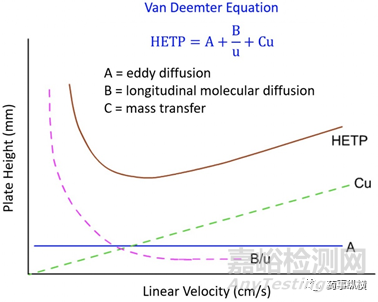
由公式我們可以將VanDeemter方程(即柱效方程)理解成是由A、B/u����、Cu三部分復(fù)合而成的曲線方程�。以流速(cm/s)為x軸,以塔板高度HETP(mm)為y軸�,分別對(duì)HETP=A��,HETP=B/u����,HETP=Cu����,HETP=A+B/u+Cu作圖�,可得如下曲線圖�。
圖1van Deemter H/u 曲線
接下來分別對(duì)公式中的A�,B��,C進(jìn)行闡述說明。
二�、渦流擴(kuò)散效應(yīng)
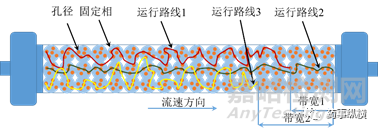
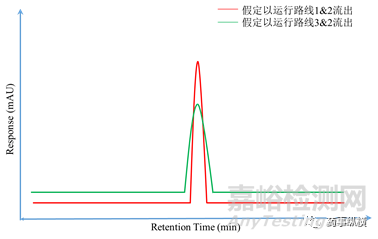
Van Deemter方程中的A項(xiàng)稱之為渦流擴(kuò)散項(xiàng)(Eddydiffusion)�,描述了由于色譜柱中固定相粒子的存在而引起的峰展寬��。通俗的解釋就是:色譜柱當(dāng)中滿充固定相填料��,而這些填料的存在會(huì)阻礙溶質(zhì)分子運(yùn)行,填料粒徑越大����,溶質(zhì)分子“繞行”距離就越遠(yuǎn)�,或在填料孔徑中停留的時(shí)間就越長(zhǎng)����。如圖2所示�,假設(shè)運(yùn)行路線2為理想運(yùn)行路線(長(zhǎng)直路線幾乎無(wú)繞行),運(yùn)行路線1和運(yùn)行路線3為非理想運(yùn)行路線(繞行明顯)����。當(dāng)溶質(zhì)分子沿路線2和路線1流出時(shí)�,此時(shí)譜帶寬度較?���。▓D2中標(biāo)示為“帶寬1”),離散程度較小�,將得到如圖3所示譜帶展寬較小的紅色流出譜圖;當(dāng)溶質(zhì)分子沿路線2和路線3流出時(shí)�,譜帶寬度較大(圖2中標(biāo)示為“帶寬2”)����,離散程度較大�,將得到如圖3所示譜帶展寬較嚴(yán)重的綠色流出譜圖����。因此渦流擴(kuò)散效應(yīng)亦被稱作“多路徑效應(yīng)”����。該效應(yīng)與填料的粒徑����、形狀��、孔徑的形狀及結(jié)構(gòu)有關(guān)�,而與流速的大小無(wú)關(guān)����。填料粒徑越大�、填料形狀越不規(guī)則�、孔徑的形狀與結(jié)構(gòu)越不規(guī)整����,溶質(zhì)分子的多路徑效應(yīng)越發(fā)明顯�,離散程度越大����,柱效越低,峰展寬越嚴(yán)重�。
圖2渦流擴(kuò)散示意圖
圖3渦流擴(kuò)散對(duì)流出譜圖展寬的影響示意圖
三����、縱向擴(kuò)散效應(yīng)
Fick定律:
J為擴(kuò)散通量��,用于量度微元時(shí)間內(nèi)物質(zhì)流過一個(gè)微元面積的量����;
D為擴(kuò)散系數(shù)�;
∅為溶質(zhì)濃度�;
x為溶質(zhì)分子遷移的位置長(zhǎng)度
VanDeemter方程中的B項(xiàng)稱之為縱向擴(kuò)散項(xiàng)(LongitudinalDiffusion)。為解釋縱向擴(kuò)散效應(yīng)�,我們?cè)诖艘隖ick定律[2]:由Fick定律可知����,擴(kuò)散通量與擴(kuò)散系數(shù)以及濃度梯度(∂ø/ax)成正比�。也就是說縱向擴(kuò)散項(xiàng)與擴(kuò)散系數(shù)以及濃差成正比����。也就是說縱向擴(kuò)散項(xiàng)與擴(kuò)散系數(shù)以及濃差成正比。根據(jù)Einstein-Smoluchowski關(guān)系式可知擴(kuò)散系數(shù)D的大小取決于絕對(duì)溫度�、分子的大小�、流體的粘度以及分子的流速����。從而可以得出如下結(jié)論:當(dāng)流速增加或溫度降低時(shí)��,擴(kuò)散系數(shù)越小����,擴(kuò)散通量越小��,縱向擴(kuò)散效應(yīng)越不明顯��,反之,當(dāng)流速減小或溫度增加時(shí)����,擴(kuò)散系數(shù)越大,擴(kuò)散通量越大�,縱向擴(kuò)散效應(yīng)越明顯�。
Einstein-Smoluchowski關(guān)系式
KB為玻爾茲曼常數(shù),為絕對(duì)溫度
r為溶質(zhì)分子的半徑
µ為流動(dòng)相的粘度
u為溶質(zhì)分子的遷移速度
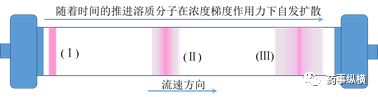
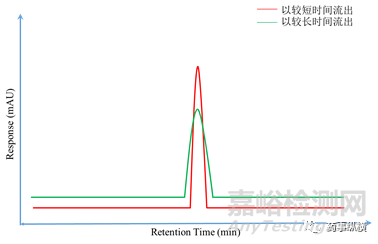
為了直觀的說明縱向擴(kuò)散效應(yīng)����,接下來將結(jié)合圖3進(jìn)行說明�。假定玫粉色的深淺代表溶質(zhì)分子濃度分布的差異�,越深濃度越大�,越淺濃度越小�。溶質(zhì)分子剛進(jìn)入色譜柱入口時(shí)�,溶質(zhì)分子集中在(Ⅰ)區(qū),未發(fā)生縱向擴(kuò)散(深玫粉色區(qū)域)��。由于(Ⅰ)區(qū)左右側(cè)(空白區(qū)域)無(wú)溶質(zhì)分子的存在,此時(shí)濃差效應(yīng)明顯����,即梯度(∂ø/ax)作用力明顯��,溶質(zhì)分子向空白區(qū)域擴(kuò)散��,呈現(xiàn)出(Ⅱ)區(qū)溶質(zhì)分子的分布狀態(tài)(中心深玫粉色區(qū)域變窄�,左右兩側(cè)呈現(xiàn)對(duì)稱的淺玫粉色區(qū)域)����。隨著時(shí)間的推進(jìn)����,溶質(zhì)分子即將離開色譜柱時(shí)�,呈現(xiàn)出(Ⅲ)區(qū)溶質(zhì)分子的分布狀態(tài)(中心深玫粉色區(qū)域進(jìn)一步變窄,左右兩側(cè)呈現(xiàn)對(duì)稱的淺玫粉色區(qū)域展寬)�。對(duì)于一個(gè)指定的色譜柱����,當(dāng)流速增大時(shí),溶質(zhì)分子將以較短的時(shí)間通過色譜柱����,此時(shí)用于縱向擴(kuò)散的時(shí)間就相應(yīng)減少,將會(huì)得到如圖4所示譜帶展寬較小的紅色流出譜圖����;反之����,流速小,溶質(zhì)分子將會(huì)以較長(zhǎng)的時(shí)間通過色譜柱��,用于縱向擴(kuò)散的時(shí)間相應(yīng)增加�,最終會(huì)得到圖4中譜帶展寬較嚴(yán)重的綠色流出譜圖�。
圖3縱向擴(kuò)散示意圖
圖4縱向擴(kuò)散對(duì)流出譜圖展寬的影響示意圖
四�、傳質(zhì)效應(yīng)
Van Deemter方程中的C項(xiàng)稱之為傳質(zhì)阻力項(xiàng)(MassTransfer)。與分離過程中樣品組分在固定相和流動(dòng)相之間的傳質(zhì)有關(guān)�。
當(dāng)流動(dòng)相在色譜柱中流動(dòng)時(shí),如果不考慮固定相的作用�,我們可以假定此時(shí)流動(dòng)相在柱腔做層流運(yùn)動(dòng)。根據(jù)Poiseuille定律[4]����,此時(shí)流動(dòng)相在色譜柱中的流速分布可以用
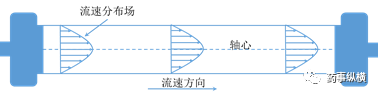
這也就是說流速和半徑之間呈現(xiàn)二次拋物線關(guān)系��,色譜柱軸心處存在最大流速�。據(jù)此我們可以形象的畫出色譜柱中的流速分布情況�,如圖5所示。通過上述的分析��,也就是說在流動(dòng)相中的溶質(zhì)分子存在同流動(dòng)相相同的速度場(chǎng)分布��,而不同的流速分布就造成了溶質(zhì)分子的傳質(zhì)過程的差異—色譜柱中心的溶質(zhì)分子傳質(zhì)速率快�,距離色譜柱中心越遠(yuǎn)傳質(zhì)速率越慢�,從而造成了流動(dòng)相中溶質(zhì)分子的譜帶展寬。而且展寬效應(yīng)會(huì)隨著流速的增大而增大����。
圖5不考慮固定相的影響色譜柱中流速分布示意圖
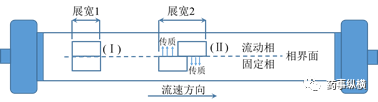
圖6流動(dòng)相/固定相中溶質(zhì)分布示意圖
根據(jù)色譜學(xué)中的速度理論可知����,流動(dòng)相與固定相中的溶質(zhì)分子的傳質(zhì)速率并不是無(wú)限大的,也就是說兩相之間的分配平衡并不是在一瞬間就完成的��,這個(gè)分配過程需要足夠的時(shí)間去完成�。如圖6所示,假定(Ⅰ)區(qū)起始溶質(zhì)分子在兩相中的展寬一致(展寬1)�,經(jīng)過一定的時(shí)間��,流動(dòng)相中的溶質(zhì)分子以初始的速率繼續(xù)運(yùn)動(dòng)�,而固定相中的溶質(zhì)分子由于“保留作用”將會(huì)以較慢速率運(yùn)動(dòng)或發(fā)生停滯從而造成譜帶的繼續(xù)展寬,如圖6中的(Ⅱ)區(qū)所示(展寬2)�。這個(gè)過程中�,為了維持流動(dòng)相與固定相中溶質(zhì)分子的局部分配平衡,流動(dòng)相中的溶質(zhì)分子將會(huì)穿過相界面?zhèn)髻|(zhì)至固定相被吸附��,而固定相中的溶質(zhì)分子則會(huì)脫附并穿過相界面?zhèn)髻|(zhì)至流動(dòng)相����。隨著流速的增加�,流動(dòng)相中的溶質(zhì)傳質(zhì)速度增加,而用于兩相平衡的相對(duì)時(shí)間減小��,最終造成譜帶的嚴(yán)重展寬。反之��,流速減小�,流動(dòng)相中的溶質(zhì)傳質(zhì)速率減慢����,而用于兩相分配平衡的相對(duì)時(shí)間增加��,最終減弱譜帶的展寬現(xiàn)象��。
五��、結(jié)束語(yǔ)
通過對(duì)vanDeemter方程的分析��,可以得出色譜柱之間存一個(gè)最優(yōu)線速度,此時(shí)可獲得最低的塔板高度及最優(yōu)的柱效����。也就是說在此速度下可獲得最優(yōu)的縱向擴(kuò)散—傳質(zhì)效應(yīng)。填料粒徑越小越均一��,渦流擴(kuò)散效應(yīng)(多路徑效應(yīng))越不明顯����。
六�、參考文獻(xiàn)
[1] van Deemter JJ, Zuiderweg FJand Klinkenberg A. Longitudinal diffusion and resistance to mass transfer ascauses of non ideality in chromatography. Chem. Eng. Sc. 1956, 5: 271–289. doi:10.1016/0009-2509(56)80003-1
[2] Adolph Fick, V. On liquiddiffusion. The London, Edinburgh, and Dublin Philosophical Magazine and Journalof Science. (1855), 10, 30.
[3] MA Islam, Einstein-Smoluchowskidissusion equation: a discussion. Physica Scripta 70 (2-3), 120, 2004.
[4] Salvatore P Sutera, RichardSkalak, The history of Poseuille’s law. Annual review of fluid mechanics 25(1), 1-20, 1993.