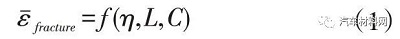摘要:針對超高強(qiáng)鋼冷成形開裂的理論分析與預(yù)測問題,歸納了現(xiàn)有理論模型的特點(diǎn)�、適用范圍及其在超高強(qiáng)鋼成形斷裂失效分析的應(yīng)用現(xiàn)狀,指出由于超高強(qiáng)鋼的脆性化傾向?qū)е缕鋽嗔逊治龃嬖诘碾y點(diǎn)�。基于超高強(qiáng)鋼的材料特性及其準(zhǔn)脆性斷裂的本質(zhì)�,對成形開裂理論預(yù)測模型與數(shù)值模擬方法提出建議�。
關(guān)鍵詞:高強(qiáng)鋼 塑性成形 斷裂失效 理論模型
1�、 前言
金屬成形過程的斷裂失效一直是工程界關(guān)注的重點(diǎn)問題。作為目前汽車領(lǐng)域最經(jīng)濟(jì)可行的輕量化手段�,高強(qiáng)鋼的應(yīng)用日益廣泛且強(qiáng)度指標(biāo)不斷提升。但高強(qiáng)鋼成形時具有與普通鋼截然不同的斷裂失效表現(xiàn)�,如斷前無明顯頸縮�、剪切斷裂以及邊緣開裂等,使得傳統(tǒng)的斷裂理論模型及適用于頸縮失效的成形極限圖(FLD)手段均無法準(zhǔn)確預(yù)測高強(qiáng)鋼板的成形開裂�。與此同時,高強(qiáng)鋼種類的多樣化以及成形加載路徑的復(fù)雜化�,對其斷裂失效的分析提出了更為嚴(yán)苛的要求。目前�,對超高強(qiáng)鋼的成形斷裂尚無準(zhǔn)確可靠的理論預(yù)測模型,給汽車關(guān)鍵零部件及其成形工藝設(shè)計(jì)帶來了嚴(yán)峻挑戰(zhàn)�。
本文首先歸納了韌性斷裂模型的發(fā)展及其在高強(qiáng)鋼成形方面的應(yīng)用現(xiàn)狀,指出了超高強(qiáng)鋼斷裂理論分析的難點(diǎn)�。從超高強(qiáng)鋼的材料特性及其脆性斷裂本質(zhì)的角度出發(fā),對超高強(qiáng)鋼成形開裂理論預(yù)測模型開發(fā)以及數(shù)值模擬方法提出建議�。
2 基于韌性斷裂損傷理論的耦合/非耦合模型
迄今為止,對高強(qiáng)鋼成形的斷裂分析和預(yù)測主要基于傳統(tǒng)韌性斷裂(損傷)理論�。這些理論可分為3 類:基于細(xì)觀孔洞形核、長大和聚合的多孔材料模型�,連續(xù)介質(zhì)損傷模型,唯象模型�。前2 類考慮了損傷演化對塑性的影響�,屬于耦合模型�,但由于在傳統(tǒng)塑性本構(gòu)模型中耦合了損傷變量,給模型求解和參數(shù)標(biāo)定增加了難度�,不易融入有限元代碼。第3 類模型則獨(dú)立考慮斷裂(損傷)變量�,忽略斷裂(損傷)演化對材料斷裂之前強(qiáng)度的影響,因此是非耦合模型�。
2.1 多孔材料模型
多孔材料模型是基于孔洞理論,即基于物理推導(dǎo)的模型�,主要包括以Gurson 模型為代表的細(xì)觀損傷模型[1],以及McClintock[2]模型�、Rice-Tracey[3]模型、GNT(Gurson-Tvergaard-Needleman)模型以及剪應(yīng)力修正的Gurson 模型等�。
1977 年,Gurson 在McClintock�、Rice-Tracey 的孔洞生長模型基礎(chǔ)上,為避開對細(xì)觀和宏觀耦合處理的困難�,采用多孔材料的正則法則等連續(xù)介觀思想,建立了含微孔材料連續(xù)介質(zhì)單元體的體胞模型�。由于Gurson 模型未考慮細(xì)觀剪切帶與孔洞擴(kuò)展之間的交互作用,因此Tvergaard和Needleman[4]引入損傷函數(shù)來考慮材料失效時孔洞的迅速聚合�,修正為GTN 模型。但GTN 模型認(rèn)為孔洞的長大是導(dǎo)致最終斷裂的微觀機(jī)制�,忽略了由剪切引發(fā)的微孔洞生長被抑制的因素。LI 等[5]將GTN 模型應(yīng)用于旋壓過程�,表明GTN 模型適合預(yù)測材料隆起區(qū)的宏觀裂紋,但不能預(yù)測負(fù)應(yīng)力三軸度下變形區(qū)域的損傷演化�。因此�,近年來將剪切損傷引入GTN 模型。如XUE 等[6]考慮了損傷演變與第三偏應(yīng)力不變量之間的相關(guān)性�,使得改進(jìn)后的GTN 模型集成了孔洞的剪切效應(yīng),適合描述低應(yīng)力三軸度下的孔洞剪切機(jī)制�。ZHOU 等[7]提出了修正的GTN 模型,將剪切損傷作為獨(dú)立的損傷變量�。然而,由于負(fù)應(yīng)力三軸度作用下剪切擴(kuò)展會加速損傷積累�,改進(jìn)的GTN 模型通常會給出更提前的斷裂預(yù)測�。對此,WU 等[8]將斷裂應(yīng)變重新定義為應(yīng)力三軸度的函數(shù)�,并對負(fù)應(yīng)力三軸度下的孔洞形核函數(shù)進(jìn)行修正,建立了更準(zhǔn)確的適合于低應(yīng)力三軸度η <-1/3 的損傷演化預(yù)測模型�。
2.2 連續(xù)介質(zhì)損傷力學(xué)模型
連續(xù)介質(zhì)損傷力學(xué)(Continuum Damage Mechanics,CDM)通過建立一個損傷演變方程來表征一個連續(xù)損傷變量,借此描述局部微觀缺陷的演變�,并且損傷效應(yīng)被直接引入到材料的本構(gòu)模型中,以此描述材料的劣化過程[9]�。CDM 考慮了損傷演化對材料塑性造成的影響�,也屬于耦合型模型。
CDM 的框架最早由法國學(xué)者LEMAITRE[10]建立�,他采用剛度退化來描述材料在線性加載條件下的損傷,推導(dǎo)了一種基于連續(xù)損傷變量�、等效應(yīng)力和熱力學(xué)體系的各向同性塑性損傷模型�。然而�,由于沒有考慮剪切帶局部化效應(yīng),基于CDM 的韌性斷裂模型可能會導(dǎo)致復(fù)雜加載條件下?lián)p傷演化的預(yù)測偏差[11]�。為此,CAO 等[12]提出了一種修正的基于應(yīng)力三軸度的LEMAITRE 損傷模型�,用于預(yù)測低應(yīng)力三軸度和剪切主導(dǎo)載荷下的韌性斷裂,同時提出一種獲得由低到高的寬范圍應(yīng)力三軸度下?lián)p傷模型參數(shù)的方法�。LIAN 等[13]以唯象的方式對傳統(tǒng)的各向同性硬化LEMAITRE 損傷模型進(jìn)行修正,考慮Lode 角對韌性斷裂的影響以及在塑性變形過程中損傷引起的軟化效應(yīng)�。YUE 等[14]采用包含Lode 角和微裂紋閉合效應(yīng)的完全耦合延性損傷模型以及混合非線性各向同性和動態(tài)硬化的模型來探究DP600 鋼在不同加載路徑下的斷裂行為。NGUYEN[15]通過引入Lode 參數(shù)來定義加載不對稱條件�,從唯象的角度考慮了剪切效應(yīng)�,提出了一種評估板料成形性能的連續(xù)損傷斷裂模型。HUANG[16]通過考慮剪切效應(yīng)的材料屈服面特性�,建立了考慮Lode 參數(shù)影響的連續(xù)損傷模型(LCDM)。
2.3 非耦合的韌性斷裂準(zhǔn)則
非耦合準(zhǔn)則單純依據(jù)韌性斷裂微觀機(jī)理構(gòu)建斷裂發(fā)生時應(yīng)力狀態(tài)變量與應(yīng)變狀態(tài)變量之間應(yīng)滿足的數(shù)學(xué)關(guān)系�,不考慮損傷與塑性變形相互耦合[17]�。主要包括最大切應(yīng)力準(zhǔn)則�、Cockcroft-Latham�、Johnson-Cook�、GISSMO 以及修正的Mohr-Coulomb(MMC)唯象型模型,以及基于經(jīng)驗(yàn)的斷裂成 形 極 限 圖(FFLD)�、Bao-Wierzbicki、Xue-Wierzbicki 斷裂模型[18]�。
早期的韌性斷裂準(zhǔn)則主要考慮宏觀力學(xué)影響因子(如第一主應(yīng)力、等效應(yīng)力�、靜水應(yīng)力或其中的多個組合)對斷裂的影響。COCKCROFT 和LATHAM[19]認(rèn)為�,斷裂主要與材料的最大主應(yīng)力有關(guān),當(dāng)斷裂位置的單位體積拉伸應(yīng)變能達(dá)到臨界破壞值時�,材料發(fā)生斷裂�。OH 等[20]采用二維孔洞模型,對C-L 準(zhǔn)則中的臨界斷裂應(yīng)變能進(jìn)行了修正解釋�,將該準(zhǔn)則成功應(yīng)用于軸對稱擠壓和拉拔工藝中�。OYANE 等[21]描述了無孔材料和多孔材料韌性斷裂的判據(jù),給出了這些準(zhǔn)則中材料常數(shù)的估算方法,并闡明了靜水應(yīng)力對斷裂應(yīng)變的影響機(jī)制�。JOHNSON 和COOK[22]以無氧高導(dǎo)電性銅、工業(yè)純鐵�、40CrNi2MoA 試樣在不同應(yīng)變率下的扭轉(zhuǎn)試驗(yàn)�、一定溫度范圍內(nèi)的霍普金森桿試驗(yàn)以及各種缺口試樣的準(zhǔn)靜態(tài)拉伸試驗(yàn)數(shù)據(jù)為對象,建立了考慮應(yīng)變�、應(yīng)變速率和溫度因素的累積損傷模型。但Johnson-Cook 模型以線性方式計(jì)算損傷積累�,但實(shí)際中大多數(shù)零部件的損傷失效是以非線性方式積累�。CLIFT 等[23]利用單位體積廣義塑性功的臨界值作為起裂條件,并用有限元模擬方法較為準(zhǔn)確地預(yù)測了鐓粗�、軸對稱擠壓和拉伸3 種不同變形條件下材料的破裂。KO 等[24]對于傳統(tǒng)韌性斷裂準(zhǔn)則預(yù)測中心翻孔破裂不準(zhǔn)確的情況�,綜合考慮了Cockcroft準(zhǔn)則中最大主應(yīng)力對損傷的影響以及Oyane 準(zhǔn)則中應(yīng)力三軸度對斷裂的影響,建立了一種新的韌性斷裂準(zhǔn)則�。
研究表明,材料斷裂行為受到多種因素的綜合影響�,如應(yīng)變路徑、損傷積累方式�、應(yīng)變率�。GISSMO 斷裂失效模型是一種基于應(yīng)變路徑的唯象模型�,它綜合考慮了材料在不同受力狀態(tài)下不同的臨界失效應(yīng)變值、非線性應(yīng)變路徑及非線性損傷積累�,反映了材料從受損開始、到損傷積累直至斷裂的整個過程�,因此可以較精確地描述材料變形過程以非線性損傷積累的失效。GISSMO 模型應(yīng)用簡便�,已廣泛應(yīng)用于金屬材料的斷裂仿真評價(jià)中。
經(jīng)典非耦合韌性斷裂模型大都局限在高應(yīng)力三軸度范圍內(nèi)�,即η取值為1/3~2/3,不能在較大的應(yīng)力三軸度范圍內(nèi)取得準(zhǔn)確的預(yù)測結(jié)果�。研究發(fā)現(xiàn),在低應(yīng)力三軸度下�,材料(特別是高強(qiáng)鋼)仍可能發(fā)生斷裂�。以BAO 和WIERZBICKI[25]為代表�,為研究應(yīng)力狀態(tài)對AA2024-T351 韌性斷裂的影響,設(shè)計(jì)了11 種具有不同幾何形狀的試樣�,進(jìn)行了壓縮試驗(yàn)、剪切試驗(yàn)和拉伸試驗(yàn)�,獲得了-0.3 <η <0.9 應(yīng) 力 三 軸 度 范 圍 內(nèi) 材 料 的 斷 裂 應(yīng)變。不同試樣斷裂結(jié)果表明:斷裂應(yīng)變與應(yīng)力三軸度η 的關(guān)系并不是單調(diào)遞減的。在負(fù)應(yīng)力三軸度(η <0)的壓縮試驗(yàn)中發(fā)生的是拉長/扭轉(zhuǎn)的剪切型韌性斷裂�;在高應(yīng)力三軸度(η >1/3)的缺口拉伸試驗(yàn)中發(fā)生的是孔洞長大的拉伸型韌性斷裂;在介于二者之間的低應(yīng)力三軸度條件下( 0 <η <1/3)�,發(fā)生的是拉伸型和剪切型復(fù)合的韌性斷裂[26]。BAO 和WIERZBICKI 的研究促進(jìn)了韌性斷裂研究領(lǐng)域的快速發(fā)展�,后續(xù)許多學(xué)者開始將剪切作用機(jī)制引入韌性斷裂準(zhǔn)則,為考慮偏應(yīng)力對斷裂的影響�,引入Lode 參數(shù)的概念,試圖建立適用范圍更廣和準(zhǔn)確性更高的新型韌性斷裂準(zhǔn)則�。例如,XUE 等[27]應(yīng)用近年來發(fā)展的塑性損傷理論�,將應(yīng)力三軸度和Lode 角相關(guān)性納入材料的非線性損傷規(guī)律和材料劣化中,利用新模型成功預(yù)測出2024-T351 鋁合金三點(diǎn)彎曲時的剪切開裂模式�。GAO 等[28]描述了一種包含靜水應(yīng)力以及應(yīng)力偏張量第二和第三不變量函數(shù)的各向同性韌性斷裂模型,并對該模型進(jìn)行了校準(zhǔn)和驗(yàn)證。BAI 和WIERZBICKI[29]從屈服面與斷裂軌跡的相似性角度出發(fā)�,在等效斷裂應(yīng)變空間、應(yīng)力三軸度空間和Lode 參數(shù)空間中建立了一個新的三維非對稱韌性斷裂模型�。此后�,BAI 等[30]基于描述脆性斷裂的Mohr-Coulomb 準(zhǔn)則,引入包含應(yīng)力三軸度�、Lode 參數(shù)與等效塑性應(yīng)變的權(quán)函數(shù)�,提出了修正MMC 模型,MMC 斷裂準(zhǔn)則可以很好地克服傳統(tǒng)成形極限圖在預(yù)測剪切斷裂時的局限性�,但當(dāng)材料不符合σˉ=Aεˉn 應(yīng)力應(yīng)變關(guān)系時,預(yù)測效果不佳�。為了提高模型預(yù)測的準(zhǔn)確性,MOHR 和MARCADET[31]將Mohr-Coulomb 中的Tresca 等效應(yīng)力轉(zhuǎn)換為Hosford等效應(yīng)力�,建立了Hosford-Coulomb 準(zhǔn)則(H-C 模型),通過試驗(yàn)證明H-C 模型克服了MMC 模型的局限性�,可以較為準(zhǔn)確地預(yù)測先進(jìn)高強(qiáng)鋼的韌性斷裂起始位置。LIAN 等[32]在Bai-Wierzbicki 模型基礎(chǔ)上�,建立修正的應(yīng)力三軸度和Lode 角影響的損傷起裂準(zhǔn)則來描述微觀尺度下材料的軟化直至開裂過程。2012 年�,LOU 與HUH[33]提出了一種新的韌性斷裂準(zhǔn)則來表征板料在塑性變形過程中孔洞的形核(等效塑性應(yīng)變的函數(shù))�、長大(應(yīng)力三軸度的函數(shù))和剪切貫通(由歸一化最大剪應(yīng)力控制)的斷裂行為�,該模型將應(yīng)力三軸度的臨界值賦予恒定的-1/3�,認(rèn)為應(yīng)力三軸度低于該值下,不會發(fā)生斷裂�。2014 年他們拓展了該準(zhǔn)則[34],基于孔洞形核�、生長和剪切貫通的微觀機(jī)理�,提出了一種宏觀韌性斷裂準(zhǔn)則�,為應(yīng)力三軸度賦予一個可變的截?cái)嘀祦肀碚魑⒂^組織�、Lode 參數(shù)�、溫度和應(yīng)變率對金屬韌性的影響�,準(zhǔn)確預(yù)測了從鐓粗到平面應(yīng)變拉伸不同應(yīng)力三軸度下AA2024-T351 的斷裂行為�。穆磊[35]提出了一個基于孔洞形核和變形機(jī)制的非耦合型韌性斷裂預(yù)測模型,使用無量綱化的最大主應(yīng)力和無量綱化的最大剪應(yīng)力來描述孔洞的長大機(jī)制和拉長扭轉(zhuǎn)機(jī)制�,將模型由主應(yīng)力空間轉(zhuǎn)化到由應(yīng)力三軸度、Lode 參數(shù)和臨界斷裂應(yīng)變構(gòu)成的三維空間�,獲得了基于該模型的三維韌性斷裂曲面模型。
研究表明�,剪切斷裂行為與材料組織均勻性有關(guān)�,例如同種強(qiáng)度的雙相鋼�,馬氏體分布越均勻越不容易產(chǎn)生剪切斷裂[36]。目前對剪切斷裂的研究主要還是在應(yīng)力應(yīng)變關(guān)系以及韌性斷裂準(zhǔn)則等宏觀的力學(xué)性能上�。邊緣開裂則歸因于剪切工藝造成的邊部微觀缺陷對后續(xù)成形過程中材料的變形產(chǎn)生的影響,如切邊質(zhì)量較差的試樣伸長率比切邊質(zhì)量好(實(shí)質(zhì)是減小剪切斷面微裂紋)的試樣低10%[37]�。通過不同的方式將材料的微觀組織結(jié)構(gòu)以及沖裁過程造成的邊緣材料的殘余應(yīng)力�、塑性應(yīng)變�、初始損傷�、幾何形貌引入到后續(xù)成形的仿真研究中[38-41],在簡單加載路徑的零件成形上實(shí)現(xiàn)了較好的預(yù)測效果�。表1 為一些基于應(yīng)變(力)的代表性斷裂準(zhǔn)則。
2.1 熱水燙種消毒:先將蔬菜種子裝入尼龍網(wǎng)袋中�,再用30℃左右的溫水浸種30分鐘�,促使種子上的病菌活化,這樣容易殺死病菌�。同時應(yīng)不斷搓洗�,以洗掉種子上所帶的抑制發(fā)芽的物質(zhì),而且也可使帶茸毛(番茄)的種子濕透�,以增加燙種效果。
3�、 高強(qiáng)鋼冷成形斷裂特點(diǎn)及其理論預(yù)測難點(diǎn)
經(jīng)典斷裂力學(xué)認(rèn)為,材料或構(gòu)件中不可避免地存在裂紋�、夾雜等各種缺陷。這些缺陷在外力作用下的擴(kuò)展演化行為與材料特性密切相關(guān)�,并由此建立針對脆性材料的線彈性和針對韌性材料的彈塑性兩類理論[9]。隨著高強(qiáng)鋼強(qiáng)度級別不斷提升�,成形時其材料屬性已進(jìn)入事實(shí)上的“脆性”范疇(如延伸率<5%)�,且高強(qiáng)鋼強(qiáng)化相馬氏體體積分?jǐn)?shù)越高,脆性斷裂趨勢越大[42]�。事實(shí)上�,從塑性變形的開始直至斷裂�,脆性材料與韌性材料在微觀組織演化與宏觀力學(xué)行為方面均存在著本質(zhì)的差異。
a.斷裂前塑性變形階段的微觀組織性能演化不同�。客觀上�,實(shí)際材料均存在一定程度的不均勻?qū)傩?。但韌性材料在外載荷作用下�,可發(fā)生大范圍�、大程度的塑性流動變形�,此階段加工硬化的組織性能演化機(jī)制具有將材料內(nèi)在不均勻性“分散”與“平均化”的趨勢�,從而使材料在失穩(wěn)斷裂前呈現(xiàn)一定“均質(zhì)性”,因此材料可假設(shè)為“勻質(zhì)”并用塑性應(yīng)變確定其斷裂閾值�。
反之,脆性材料成形時只能發(fā)生小范圍的塑性流動�,原始微觀非均勻缺陷(包括板側(cè)的毛刺)的影響無法轉(zhuǎn)移,因此對初始缺陷更加敏感�。這也解釋了材料特性與邊緣開裂趨勢的內(nèi)在聯(lián)系:韌性好的低強(qiáng)度級別材料可通過協(xié)調(diào)性變形弱化邊部缺陷,邊部開裂可能性較??;隨著強(qiáng)度級別提高,材料對邊緣微觀缺陷敏感性增加�,因此高強(qiáng)鋼容易出現(xiàn)邊緣開裂�。
b.宏觀的斷裂表現(xiàn)不同。材料原始微觀缺陷理論上是隨機(jī)分布的�。脆性材料由于變形量小而無法使缺陷效應(yīng)“平均化”,性能參數(shù)試驗(yàn)值分散度很大�,且測量誤差相對于整體應(yīng)變的占比較大。因此�,由于脆性斷裂的顯著“突發(fā)性”與“隨機(jī)性”,起裂與斷裂的理論分析預(yù)測更為困難�。
迄今為止�,對高強(qiáng)鋼斷裂失效的分析大多基于韌性斷裂的思路和假設(shè)�,這難免造成結(jié)果的誤差。例如,基于細(xì)觀孔洞演化的模型可考慮應(yīng)變路徑等多因素影響�,在高強(qiáng)鋼斷裂分析中已得到應(yīng)用,但無法準(zhǔn)確分析高強(qiáng)鋼剪切斷裂�、邊緣開裂的特殊失效形式;唯象試驗(yàn)判據(jù)簡單易用�,但難以考慮變形歷史與加工硬化影響�;半經(jīng)驗(yàn)性CMD 宏觀模型考慮了與應(yīng)力/應(yīng)變相關(guān)因素�,但難以引入復(fù)雜加載路徑的影響�。材料的斷裂包括高強(qiáng)鋼的剪切斷裂被認(rèn)為由應(yīng)力狀態(tài)控制?;趹?yīng)力的韌性斷裂準(zhǔn)則認(rèn)為材料的應(yīng)力狀態(tài)達(dá)到某一臨界斷裂條件則發(fā)生斷裂�,如最大主應(yīng)力準(zhǔn)則�、最大切應(yīng)力準(zhǔn)則、M-C 準(zhǔn)則、MMC 模型等�。理論上,這類準(zhǔn)則預(yù)測脆性斷裂更具優(yōu)勢�,但由于未考慮變形過程中的應(yīng)變歷史�,同樣存在一定的局限性。此外�,斷裂是一種帶有大應(yīng)力梯度的局部現(xiàn)象,很難直接通過試驗(yàn)獲取相關(guān)區(qū)域內(nèi)與應(yīng)力相關(guān)的狀態(tài)變量�。因此�,這類準(zhǔn)則在實(shí)際應(yīng)用時�,通常根據(jù)增量理論將基于應(yīng)力的判據(jù)轉(zhuǎn)換為基于應(yīng)變的表達(dá)形式,如公式(1)�。
表1 基于應(yīng)變(力)的幾個斷裂準(zhǔn)則
注:η 為應(yīng)力三軸度;L 為Lode參數(shù)�;θˉ為羅德角參數(shù)�;A�、C1�、C2�、C3�、C4�、C5�、C6 為對應(yīng)斷裂模型的標(biāo)定參數(shù)。
此時,模型回歸到應(yīng)變空間中�,由高強(qiáng)鋼脆性造成的應(yīng)變實(shí)測分散性將引起標(biāo)定參數(shù)較大的波動性,最終亦無法準(zhǔn)確預(yù)測高強(qiáng)鋼的斷裂行為�??傮w上�,由于實(shí)際高強(qiáng)鋼成形斷裂問題的復(fù)雜性,現(xiàn)有基于“韌性”斷裂思路以及應(yīng)變(力)的失效模型的預(yù)測精度有限�。
研究發(fā)現(xiàn),高強(qiáng)鋼成形過程中會產(chǎn)生更多的局部塑性變形�,通過簡單拉伸試驗(yàn)得到的低延伸率(如<5%)或者應(yīng)變來評價(jià)高強(qiáng)鋼的成形性能具有局限性(過于保守),由此建立的恒等效應(yīng)變斷裂模型不再適用�。相比之下,考慮不同應(yīng)變路徑的成形極限圖(FLD)更為合理�。但基于縮頸失穩(wěn)理論建立的FLD 往往高估成形極限�,也無法預(yù)測邊緣開裂與剪切開裂等特殊開裂模式�。
4、 超高強(qiáng)鋼成形開裂預(yù)測理論研究思路
4.1 理論分析與預(yù)測模型
針對脆性材料的特殊斷裂機(jī)制�,已有一些異于傳統(tǒng)思路的理論嘗試。邢修三[44]將斷裂理論建立于微裂紋發(fā)展動力學(xué)的統(tǒng)計(jì)基礎(chǔ)上�,導(dǎo)出有關(guān)宏觀力學(xué)量�;謝鵬等[45]基于邊界效應(yīng)模型(BEM),并引入細(xì)觀結(jié)構(gòu)參量—平均粒徑G�,建立脆性材料細(xì)觀結(jié)構(gòu)與宏觀力學(xué)性能之間的關(guān)系�;范書群等[46]根據(jù)缺陷累計(jì)失效概率的概念得到脆性材料破壞的概率公式�;SINGH[47]利用離散與連續(xù)介質(zhì)的方法研究了脆性斷裂的一些基礎(chǔ)問題。但將脆性斷裂的思想用于高強(qiáng)鋼失效分析的研究還未見報(bào)道�,相關(guān)工作仍有待開展。
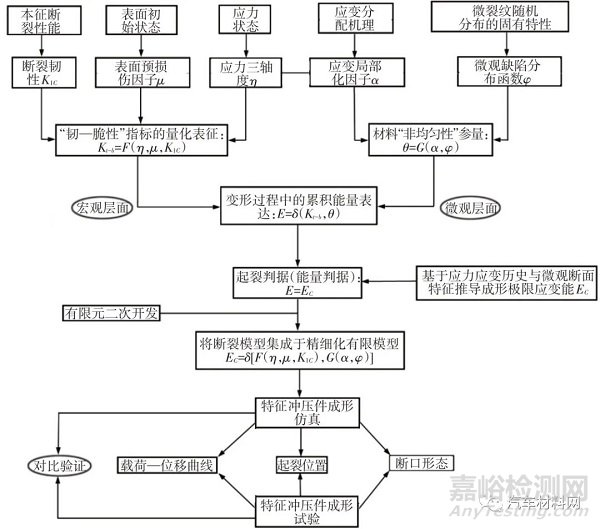
基于能量原理的力學(xué)準(zhǔn)則通常具有明顯的物理背景�,而且能夠同時考慮應(yīng)變(及歷史)、應(yīng)力因素的綜合影響�。圖1所示為基于“韌—脆性”斷裂特性的高強(qiáng)鋼失效行為多尺度精細(xì)模型構(gòu)建思路�。以高強(qiáng)鋼“韌—脆性”材料特性為核心思想�,結(jié)合微觀機(jī)制引入復(fù)雜應(yīng)力狀態(tài)下的非均勻變形行為�,并考慮宏觀隨機(jī)斷裂特性與材料初始狀態(tài)多重因素的影響�,基于能量原理(ΔE=dε×dσ)構(gòu)建針對“韌—脆性”材料的斷裂失效模型�。其中�,從高強(qiáng)鋼“韌—脆性”的材料本質(zhì)特性出發(fā)�,結(jié)合經(jīng)典斷裂力學(xué)理論,設(shè)計(jì)面向于高強(qiáng)鋼的“韌—脆性”指標(biāo)測試方法及試驗(yàn)系統(tǒng)�,分析不同復(fù)雜應(yīng)力狀態(tài)及表面初始狀態(tài)(表面預(yù)損傷)對高強(qiáng)鋼斷裂特征的影響規(guī)律�,獲取“韌—脆性”特征量化表達(dá)�。微觀方面�,針對高強(qiáng)鋼微觀組織結(jié)構(gòu),基于非平衡統(tǒng)計(jì)的概念和方法引入微觀缺陷分布函數(shù)(初始微裂紋密度分布函數(shù))�,考察裂紋演化的微觀機(jī)理,同時引入應(yīng)變局部化因子以考慮高強(qiáng)鋼在變形過程中的應(yīng)變局部化效應(yīng)�;聯(lián)立微觀缺陷分布函數(shù)和應(yīng)變局部化因子以表征材料“非均勻性”參量,進(jìn)而更為全面的揭示高強(qiáng)鋼材料微觀組織結(jié)構(gòu)對內(nèi)部裂紋萌生及擴(kuò)展的影響機(jī)制�?;趹?yīng)力/應(yīng)變歷史和微觀斷面特征推導(dǎo)成形極限應(yīng)變能�,獲取成形極限應(yīng)變能與“韌—脆性”指標(biāo)�、材料“非均勻性”參量之間的函數(shù)表達(dá)�,從能量角度構(gòu)建基于“韌—脆性”斷裂特性的高強(qiáng)鋼失效行為多尺度精細(xì)模型�。
圖1 基于“韌—脆性”斷裂特性的高強(qiáng)鋼失效行為多尺度精細(xì)模型
4.2 數(shù)值仿真
目前針對材料斷裂失效的仿真大多采用FEM(有限元法)加單元刪除法。該方法簡單高效�,但單元刪除在一定程度上會導(dǎo)致系統(tǒng)質(zhì)量和能量的損失,引起斷裂特征的模糊化�。此外�,F(xiàn)EM 模擬結(jié)果的準(zhǔn)確性也較大程度的依賴于精細(xì)化的網(wǎng)格尺寸�,在裂紋形貌方面不具優(yōu)勢。
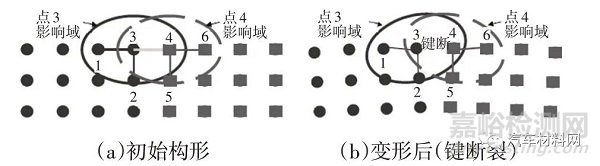
無網(wǎng)格方法是近年來興起的一類新的數(shù)值方法�,其中無單元Galerkin 法比較成熟�,并已被應(yīng)用于彈塑性問題分析[48]�。無網(wǎng)格法采用直接點(diǎn)積分與穩(wěn)定性增強(qiáng)項(xiàng)以及鍵斷裂模型,保證了質(zhì)量�、動量與能量的守恒以及數(shù)值穩(wěn)定性、收斂性�,因而能夠有效地模擬材料的失效與破壞,在模擬裂紋擴(kuò)展的非連續(xù)體問題時具有顯著優(yōu)勢�。Livermore 公司在光滑粒子伽遼金法(Smooth Particle Galerkin Method,SPG)的框架下開發(fā)了鍵斷裂模型�。SPG是采用直接點(diǎn)積分(DNI)的Galerkin 法�,它依照位移光滑理論導(dǎo)出了數(shù)值穩(wěn)定性的增強(qiáng)項(xiàng),從而抑制了弱形式常規(guī)DNI 導(dǎo)致的低能(沙漏)模式�,能夠獲得穩(wěn)定收斂的數(shù)值解,進(jìn)而可用于材料的失效與破壞分析�。如圖2 所示�,一旦材料達(dá)到失效條件�,則鍵斷開�,相應(yīng)位置積分點(diǎn)的應(yīng)力置零�,而非FEM 在應(yīng)力置零的同時刪除單元�,從而避免了能量與模型特征損失�。圖3 為本文利用SPG 方法模擬某高強(qiáng)鋼板折彎開裂的效果,結(jié)果顯示鍵斷裂處理方式在一定程度上保留了斷裂特征�。
圖2 鍵斷裂模型[48]
圖3 利用SPG方法模擬某高強(qiáng)鋼板折彎開裂
SILLING 等[49]提出的動力學(xué)法(Peridynamics�,PD)也是一種無網(wǎng)格非局部數(shù)值方法�。PD 基本方程采用積分形式代替?zhèn)鹘y(tǒng)連續(xù)介質(zhì)力學(xué)的偏微分方程,避免了空間求導(dǎo)�,在不連續(xù)處仍舊成立�,無需進(jìn)行連續(xù)性假設(shè)�,解決了奇異性和計(jì)算效率問題�,特別適合處理脆性材料的復(fù)雜破壞問題�。如圖4 所示�,任波[50]利用PD 方法準(zhǔn)確預(yù)測了汽車擋風(fēng)玻璃受沖擊作用下的破裂擴(kuò)展行為。
圖4 利用近場動力學(xué)法模擬玻璃受擊破裂[50]
鑒于無網(wǎng)格方法在模擬材料自發(fā)裂紋成核和擴(kuò)展問題中的巨大潛力�,有理由認(rèn)為�,它將在高強(qiáng)鋼斷裂仿真分析方面取得應(yīng)用�。
5�、 結(jié)束語
隨著高強(qiáng)鋼強(qiáng)度級別的不斷提升�,材料呈現(xiàn)明顯的脆性化趨勢并帶來塑性變形能力大幅下降�,其斷裂具有與韌性材料截然不同的表現(xiàn)�,如開裂的隨機(jī)性�、非均勻性以及初始缺陷的敏感性等。傳統(tǒng)基于韌性材料的斷裂準(zhǔn)則無法準(zhǔn)確分析和預(yù)測高強(qiáng)鋼成形的開裂�。鑒于超高強(qiáng)鋼的材料特性,預(yù)測其斷裂失效與成形極限需充分考慮(準(zhǔn))脆性的本質(zhì)以及與此相關(guān)的復(fù)雜加載路徑下的微觀非均勻變形與宏觀隨機(jī)斷裂特性�,并計(jì)入應(yīng)變、應(yīng)力與材料初始狀態(tài)多重因素的影響,才可能從根本上解決問題�。
參考文獻(xiàn):
[1] GURSON A L. Continuum theory of ductile rupture by void nucleation and growth: Part I yield criteria and flow rules for porous ductile media[J]. Journal of Engineering Materials and Technology,1977,99(1):2-15.
[2] MCCLINTOCK F A, KAPLAN S M, BERG C A. Ductile fracture by hole growth in shear bands[J]. International Journal of Fracture Mechanics,1966,2(4):614-627.
[3] RICE J R, TRACEY D M. On the ductile enlargement of voids in triaxial stress fields[J]. Journal of the Mechanics and Physics of Solids,1969,17(3):201-217.
[4] TVERGAARD V, NEEDLEMAN A. Analysis of the cupcone fracture in a round tensile bar[J]. Acta Metallurgica,1984,32(1):157-169.
[5] LI H, FU M W, LU J, et al. Ductile fracture: Experiments and computations[J]. International Journal of Plasticity,2011,27(2):147-180.
[6] XUE L. Constitutive modeling of void shearing effect in ductile fracture of porous materials[J]. Engineering Fracture Mechanics,2008,75(11):3343-3366.
[7] ZHOU J, GAO X S, SOBOTKA J C, et al. On the extension of the Gurson-type porous plasticity models for prediction of ductile fracture under shear-dominated conditions[J]. International Journal of Solids and Structures,2014,51(18):3273-3291.
[8]WU H,XU W C,SHAN D,et al.An extended GTN model for low stress triaxiality and application in spinning forming[J]. Journal of Materials Processing Technology, 2018,(263):112-128.
[9]溫彤.韌性損傷模型及其在金屬塑性加工中的應(yīng)用研究[D].重慶:重慶大學(xué),1999.
[10] LEMAITRE J. A continuous damage mechanics model for ductile fracture[J]. Transactions of the Asme Journal of Engineering Materials and Technology, 1985, 107(107):83-89.
[11] KHAN A S, LIU H W. A new approach for ductile fracture prediction on Al 2024-T351 alloy[J]. International Journal of Plasticity,2012(35):1-12.
[12] CAO T S, GACHET J M, MONTMITONNET P, et al. A Lode-dependent enhanced Lemaitre model for ductile fracture prediction at low stress triaxiality[J]. Engineering Fracture Mechanics,2014(124-125):80-96.
[13] LIAN J H, FENG Y , S MÜNSTERMANN. A Modified Lemaitre Damage Model Phenomenologically Accounting for the Lode Angle Effect on Ductile Fracture[J].Procedia Materials Science,2014(3):1841-1847.
[14] YUE Z , CAO K , BADREDDINE H , et al. Failure prediction on steel sheet under different loading paths based on fully coupled ductile damage model[J]. International Journal of Mechanical Sciences,2019(153-154):1-9.
[15] NGUYEN N T, KIM D Y, KIM H Y. A continuous damage fracture model to predict formability of sheet metal[J]. Fatigue and Fracture of Engineering Materials and Structures,2013(36):202-216.
[16]HUANG X W,GE J Z,ZHAO J,et al.A continuous damage model of Q690D steel considering the influence of Lode parameter and its application[J]. Construction and Building Materials,2020(262):120067.
[17]楊婷,熊自柳,孫力,等.汽車用先進(jìn)高強(qiáng)鋼韌性斷裂模型的研究與應(yīng)用進(jìn)展[J].鍛壓技術(shù),2021,46(1):10-16+23.
[18]董梁.高強(qiáng)鋼板材剪切邊緣局部成形性能表征與開裂預(yù)測研究[D].上海:上海交通大學(xué),2017.
[19] COCKCROFT M, LATHAM D. Ductility and the workability of metals[J].The Journal of the Institute of Metals,1968,96(1):33-39.
[20]OH S I,CHEN C C,KOBAYASHI S.Ductile Fracture in Axisymmetric Extrusion and Drawing—Part 2:Workability in Extrusion and Drawing[J]. Journal of Engineering for Industry,1979,101(1):36.
[21]OYANE M,SATO T,OKIMOTO K,et al.Criteria for ductile fracture and their applications[J].Journal of Mechanical Working Technology,1980,4(1):65-81.
[22] JOHNSON G R, COOK W H. Fracture characteristics of three metals subjected to various strains, strain rates,temperatures and pressures[J]. Engineering Fracture Mechanics,1985,21(1):31-48.
[23] CLIFT S E, HARTLEY P, STURGESS C, et al. Fracture prediction in plastic deformation processes[J]. International Journal of Mechanical Sciences,1990,32(1):1-17.
[24]Y K KO,J S LEE,H HUH,et al.Prediction of fracture in hub-hole expanding process using a new ductile fracture criterion[J]. Journal of Materials Processing Technology,2007(187-188):358-362.
[25] BAO Y B, WIERZBICKI T. On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanical Sciences, 2004, 46(1): 81-98.
[26]趙長財(cái),楊卓云,董國疆,等.韌性斷裂準(zhǔn)則新發(fā)展及其在輕合金板材成形中的應(yīng)用[J]. 中國有色金屬學(xué)報(bào),2020,30(8):11.
[27] XUE L, WIERZBICKI T. Ductile fracture initiation and propagation modeling using damage plasticity theory[J].Engineering Fracture Mechanics, 2008, 75(11): 3276-3293.
[28] GAO X S, ZHANG T T, ZHOU J, et al. On stress-state dependent plasticity modeling:Significance of the hydrostatic stress, the third invariant of stress deviator and the non-associated flow rule[J].International Journal of Plasticity,2011,27(2):217-231.
[29] BAI Y, WIERZBICKI T. A new model of metal plasticity and fracture with pressure and Lode dependence[J]. International Journal of Plasticity,2008,24(6):1071-1096.
[30]BAI Y,WIERZBICKI T.Application of extended Mohr-Coulomb criterion to ductile fracture[J]. International Journal of Fracture,2010,161(1):1-20.
[31]MOHR D,MARCADET S J.Micromechanically-motivated Phenomenological Hosford-Coulomb Model for Predicting Ductile Fracture Initiation at Low Stress Triaxialites[J]. International Journal of Solids and Structures,2015(67-68):40-55.
[32] LIAN J, WU J, Munstermann S. Evaluation of the cold formability of high-strength low-alloy steel plates with the modified Bai- Wierzbicki model[J]. International Journal of Damage Mechanics,2015,24(3):383-417.
[33]LOU Y S,HUH H,LIM S,et al.New ductile fracture criterion for prediction of fracture forming limit diagrams of sheet metals[J].International Journal of Solids and Structures,2012,49(25):3605-3615.
[34] LOU Y S, YOON J W, HUH H. Modeling of shear ductile fracture considering a changeable cut-off value for stress triaxiality[C]// International Journal of Plasticity,2014:56-80.
[35]穆磊.面向先進(jìn)高強(qiáng)鋼的韌性斷裂預(yù)測模型研究與應(yīng)用[D].北京:北京科技大學(xué),2018.
[36]CHOI K S,LIU W N,SUN X,et al.Influence of Manufacturing Processes and Microstructures on the Performance and Manufacturability of Advanced High Strength Steels[J]. Journal of Engineering Materials & Technology,2009,131(4):41205-41213.
[37]祝洪川,孫宜強(qiáng), 吳青松. 先進(jìn)高強(qiáng)鋼斷裂性能研究[J].鍛壓技術(shù),2015,40(12):115-119.
[38]WANG K,GREVE L,WIERZBICKI T.FE Simulation of Edge Fracture Considering Pre-damage from Blanking Process[J].International Journal of Solids and Structures,2015(71):206-218.
[39] CLIFF B, DAVID A, MICHAEL W . Predicting Failure during Sheared Edge Stretching Using a Damage-Based Model for the Shear-Affected Zone[J]. Sae International Journal of Materials & Manufacturing, 2013, 6(2): 304-312.
[40] SARTKULVANICH P, KROENAUER B, GOLLE R, et al. Finite element analysis of the effect of blanked edge quality upon stretch flanging of AHSS[J]. CIRP Annals-Manufacturing Technology,2010,59(1):279-282.
[41] UTHAISANGSUK V, PRAHL U, BLECK W. Stretchflangeability characterisation of multiphase steel using a microstructure based failure modelling[J]. Computational Materials Science,2009,45(3):617-623.
[42]羅娟娟,史文,黃群飛,等.高馬氏體量雙相鋼的組織與性能研究[J].鋼鐵,2008,43(4):84-88.
[43] WIERZBICKI T, BAO Y, LEE Y W, et al. Calibration and evaluation of seven fracture models[J]. International Journal of Mechanical Sciences,2005,47(4-5):719-743.
[44] 邢修三. 金屬穿晶脆性斷裂統(tǒng)計(jì)理論[J]. 物理學(xué)報(bào),1999(1):110-116.
[45]謝鵬,劉問,胡雨村,等.重組竹橫向準(zhǔn)脆性斷裂的斷裂參數(shù)[J].復(fù)合材料學(xué)報(bào),2020,37(6):1466-1475.
[46]范書群,李永池,王志亮.脆性斷裂的概率統(tǒng)計(jì)方法和應(yīng)用[J].力學(xué)與實(shí)踐,2007(2):57-60.
[47]SINGH G.Discrete and continuum studies of some fundamental issues in brittle fracture mechanics[D]. London:Imperial College London,2013.
[48] WU Y C, HU W, PAN X F, et al. Recent Developments of Smoothed Particle Galerkin (SPG) Method for Joint Modeling[C]// 16th International LS- DYNA® Users Conference,ANSYS SimuLive,2020.
[49] SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids,2000(48):175-209.
[50]REN B,WU C T,E ASKARI.A 3D Discontinuous Galerkin FEM with the Bond-based Peridynamics Model for Dynamic Brittle Failure Analysis[J]. International Journal of Impact Engineering,2017(99):14-25.
來源:期刊《汽車工藝與材料》作者:周銀1 溫彤1 方剛1,2 路勝海3 李冠楠4
(1.重慶大學(xué)材料科學(xué)與工程學(xué)院,重慶 400044�;2.中國汽車工程研究院股份有限公司,重慶 401122;3.河鋼集團(tuán)鋼研總院�,石家莊 050023;4.河鋼集團(tuán)邯鋼公司�,邯鄲 056015)