一���,什么是頻譜泄露��,如何減少頻譜泄露�����?
首先我們知道���,對(duì)一個(gè)N點(diǎn)的信號(hào),我們必須要做大于N點(diǎn)的fft�����,才能保證輸出正常���。(頻域采樣定理)
但是對(duì)于現(xiàn)實(shí)生活中的信號(hào)�����,很多都是無限長的�����,這也會(huì)導(dǎo)致采樣后的離散信號(hào)點(diǎn)數(shù)N也是無限大的�����,不利于我們進(jìn)行fft運(yùn)算���。因此我們需要用一些方法選出一些點(diǎn)來進(jìn)行fft運(yùn)算。
我們都知道��,頻譜與沖激函數(shù)卷積���,相對(duì)于位移但幅度互相不影響�����。
但是如果直接截出一部分點(diǎn)�����,則相當(dāng)于在原信號(hào)的基礎(chǔ)上加矩形窗�����,頻域就相對(duì)于和sa函數(shù)卷積���。卷積的過程就會(huì)污染原本的頻域��,導(dǎo)致原有頻率成分偏移到其他頻率成分上��。
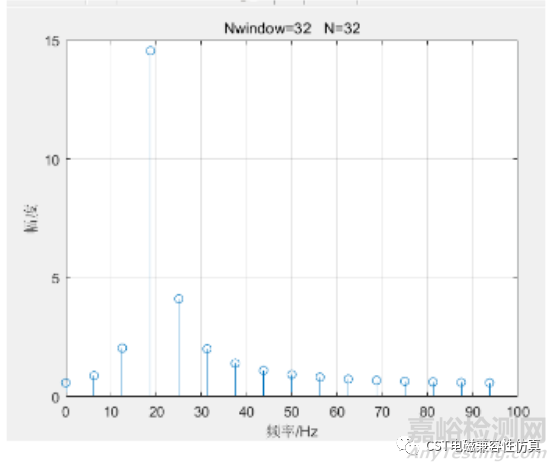
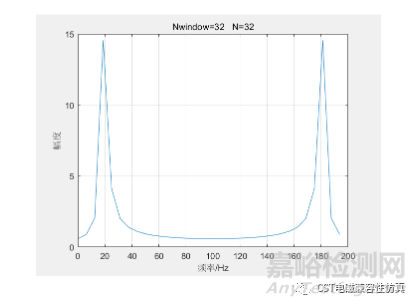
如下圖��,我們對(duì)一個(gè)頻率為20Hz的單頻三角函數(shù)加矩形窗做fs=200的32點(diǎn)fft運(yùn)算��,可以看到�����,不僅20Hz除有頻譜成分��,其他頻率成分上也有�����,這就叫做頻譜泄露��。
本文中Nwindow代表截?cái)嗪髸r(shí)域有效數(shù)據(jù)點(diǎn)數(shù)�����,N代表fft點(diǎn)數(shù)
那么該如何減小泄露呢���?
可以選擇增大信號(hào)點(diǎn)數(shù)或者選用更好的窗函數(shù)來截?cái)嘣瘮?shù)
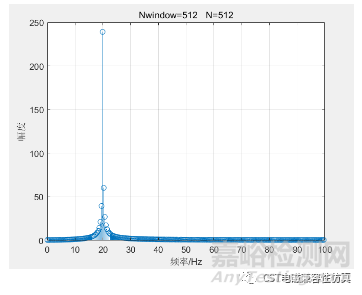
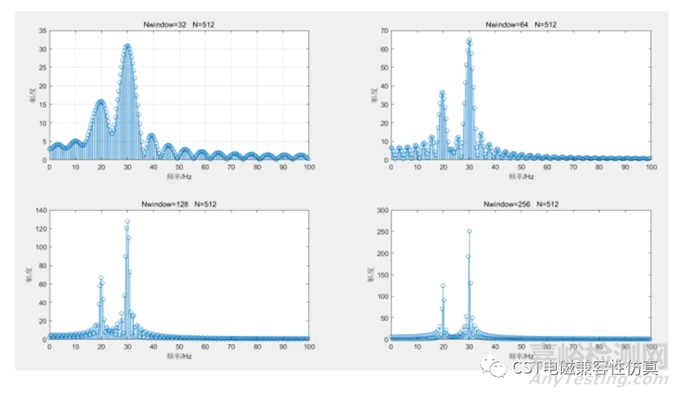
下圖是進(jìn)行512點(diǎn)fft的頻譜(同時(shí)信號(hào)有效點(diǎn)數(shù)也增大為512)
二,什么是柵欄效應(yīng)���,降低柵欄效應(yīng)���?
首先來看柵欄效應(yīng),由于DFT是在DTFT的基礎(chǔ)上對(duì)頻域進(jìn)行采樣���,因此頻域就會(huì)變成離散的點(diǎn)��,就好像通過柵欄觀察頻譜一樣�����,因此叫做柵欄效應(yīng)���。
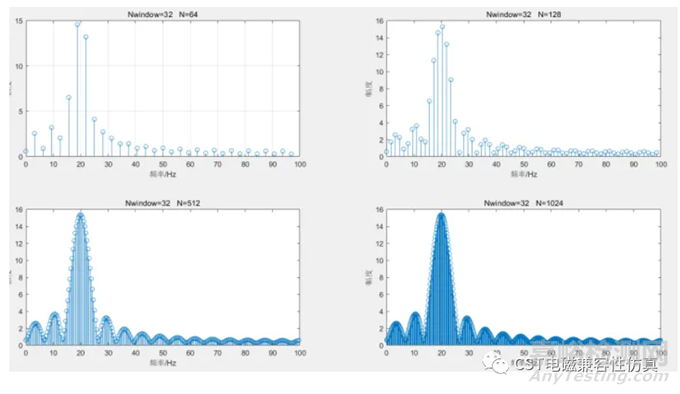
柵欄效應(yīng)可以通過時(shí)域補(bǔ)零來減小,同時(shí)也相當(dāng)于增大頻域的采樣點(diǎn)數(shù)(因?yàn)轭l域采樣點(diǎn)數(shù)等于時(shí)域信號(hào)的點(diǎn)數(shù))��。下圖是表示時(shí)域信號(hào)有效長度不變的情況下,分別補(bǔ)零不同的點(diǎn)數(shù)對(duì)應(yīng)的結(jié)果�����,可以看出補(bǔ)零越多�����,柵欄效應(yīng)越小��。
三��,什么是頻譜分辨率��,如何降低頻譜分辨率���?
頻譜分辨率是在頻率上能把兩個(gè)信號(hào)分開的能力�����。
這里有一個(gè)誤區(qū)就是補(bǔ)零可以增大頻譜分辨率���,這是錯(cuò)誤的,是錯(cuò)誤的理解了頻譜分辨率概念所引起的�����。接下來一個(gè)圖片是對(duì)兩個(gè)單頻的疊加信號(hào)做fft,我們看看通過補(bǔ)零能否增加頻譜分辨率(主瓣頂峰所對(duì)應(yīng)的距離)
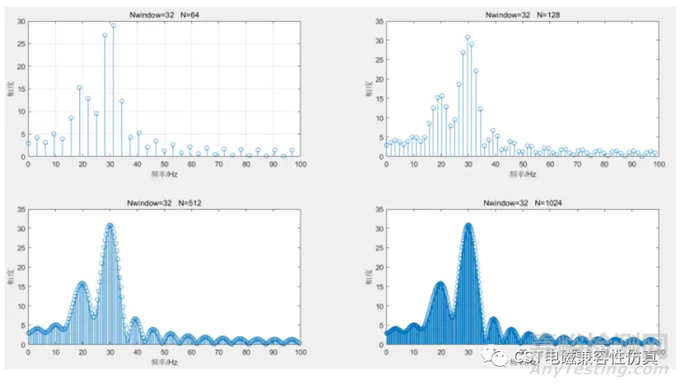
我們可以看到���,通過補(bǔ)零只能把圖像變得更平滑��,但是無法增大把20Hz,30Hz這兩個(gè)單頻信號(hào)分開的能力�����。接下來我們?cè)黾訒r(shí)域有效采樣點(diǎn)數(shù)��,觀察效果��。
可以看到�����,通過增加時(shí)域有效點(diǎn)數(shù)��,可以增大兩個(gè)單頻點(diǎn)被分辨開的能力���。
同時(shí)選用更好的窗函數(shù)也可以增大頻率分辨率���。
在這里可以聯(lián)想到頻譜泄露的概念��,實(shí)際上頻譜分辨率低也是因?yàn)槟滁c(diǎn)頻率因?yàn)轭l譜泄露而污染了另一點(diǎn)的頻率��,因此減小頻譜泄露實(shí)際上也就是增大頻譜分辨率��。他們都可以選用更好的窗函數(shù)以及增大時(shí)域有效點(diǎn)數(shù)N來優(yōu)化��。
四�����, 為什么fft之后產(chǎn)生對(duì)稱的圖像�����?
首先我們知道實(shí)信號(hào)的頻譜是對(duì)稱的���,即X(k)=X*(-k)
又有fft的頻譜具有隱含周期性,則X(k)=X(k+N)
因此 X(k)=X*(N-k) 即在一個(gè)采樣周期內(nèi)���,以一半的采樣頻率為分界線��,兩邊的值是對(duì)稱的
所以我們只需取一半點(diǎn)即可
五���,DFT中采樣頻率��,模擬頻率和數(shù)字頻率的區(qū)別和聯(lián)系
首先我們知道�����,在物理世界中只有模擬頻率f���,它的單位是Hz,這也是最容易理解的一個(gè)頻率�����。
其次我們對(duì)信號(hào)采樣有了采樣頻率fs���,并且根據(jù)奈奎斯特采樣定理,原信號(hào)的頻率是不大于0.5倍的fs的���。也就是說原模擬信號(hào)的頻率f是處于區(qū)間(0,0.5fs)的
那么我們就可以把原信號(hào)的模擬頻率區(qū)間(0���,fs)���,一一對(duì)應(yīng)到數(shù)字頻率區(qū)間(0��,2pi)��。
他們的轉(zhuǎn)化關(guān)系為w=2pi*f/fs(其中w為數(shù)字頻率�����,f為模擬頻率���,fs為采樣頻率)