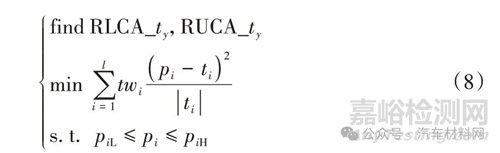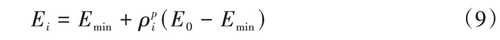[摘要] 本文構(gòu)造副車架靜剛度與K&C 性能的并行仿真流程�����,提出考慮多學(xué)科性能耦合的副車架靜剛度目標(biāo)修正方法����,并系統(tǒng)地建立一體式空心鑄鋁副車架分層級設(shè)計優(yōu)化方法����。首先�����,建立副車架計算模型并改進加載方法��,提出局部坐標(biāo)系下的靜剛度計算方法��,并集成副車架靜剛度分析、模型縮減分析����、K&C 性能分析3 種工況��,執(zhí)行多樣本分析并通過實驗設(shè)計矩陣轉(zhuǎn)換,構(gòu)建K&C 性能與靜剛度性能的組合代理模型,基于組合代理模型利用K&C性能修正靜剛度目標(biāo);其次����,開展多性能約束的副車架多層級拓?fù)鋬?yōu)化,通過第1 層級拓?fù)鋬?yōu)化完成等壁厚主體結(jié)構(gòu)設(shè)計����,通過第2層級拓?fù)鋬?yōu)化完成變壁厚結(jié)構(gòu)設(shè)計����。結(jié)果表明:經(jīng)過多層級拓?fù)鋬?yōu)化的副車架1階、2階扭轉(zhuǎn)模態(tài)分別提升39.3%����、14.9%����,靜剛度及K&C 性能滿足目標(biāo)要求����,其他各項性能指標(biāo)均得到顯著提升且實現(xiàn)輕量化����。本文可為副車架靜剛度性能目標(biāo)制定�����、K&C性能提升及副車架結(jié)構(gòu)優(yōu)化提供參考��。
關(guān)鍵詞:副車架��;靜剛度��;K&C性能;拓?fù)鋬?yōu)化;多性能約束
前言
副車架是連接車身與懸架系統(tǒng)的關(guān)鍵部件,其結(jié)構(gòu)設(shè)計要滿足多學(xué)科性能����,關(guān)于副車架設(shè)計優(yōu)化方法一直是研究的熱點[1-3]����。文獻[4]中以副車架動剛度為性能指標(biāo)��,采用尺寸優(yōu)化和形狀優(yōu)化為技術(shù)手段����,發(fā)現(xiàn)達成動剛度指標(biāo)至少需要增質(zhì)量15%����,說明在架構(gòu)不變的情況下,僅通過調(diào)整厚度和形狀來大幅提升性能會付出較大代價,有必要優(yōu)先開展拓?fù)鋬?yōu)化改善整體架構(gòu)設(shè)計;朱劍峰等[5]以后副車架硬點剛度為性能約束開展拓?fù)鋬?yōu)化,以硬點剛度����、結(jié)構(gòu)模態(tài)為性能優(yōu)化指標(biāo)開展參數(shù)設(shè)計����,對鈑金副車架設(shè)計具有重要參考價值����;馬芳武等[6]重點考慮典型載荷工況�����,采用折衷規(guī)劃法進行副車架拓?fù)鋬?yōu)化,并建立參數(shù)化模型對后副車架進行多目標(biāo)優(yōu)化�����,可以支撐概念階段鈑金副車架結(jié)構(gòu)參數(shù)化設(shè)計��。廖鶯等[7]進一步完善拓?fù)鋬?yōu)化階段的工況定義�����,并提出后副車架目標(biāo)制定方法����,經(jīng)過拓?fù)鋬?yōu)化和多學(xué)科優(yōu)化�����,輕量化效果顯著����,但拓?fù)涓拍钤O(shè)計階段要求強度這一局部性能達標(biāo)����,可能出現(xiàn)過設(shè)計問題�����,副車架剛度目標(biāo)制定采用經(jīng)驗方法無法準(zhǔn)確兼顧K&C 性能����。林佳武等[8]從碰撞性出發(fā)�����,通過拓?fù)鋬?yōu)化實現(xiàn)真空高壓鑄鋁后縱梁結(jié)構(gòu)輕量化�����,由于工藝特征和成型方法差異較大��,高壓鑄造車身部件的優(yōu)化方法不適用于低壓鑄造的底盤部件�����。
新能源汽車對高性能和輕量化的極致追求,促進集成度更高的一體式空心鑄鋁副車架的推廣和應(yīng)用��,基于上述研究的局限性��,本文提出考慮性能耦合的副車架靜剛度目標(biāo)修正方法�����,并系統(tǒng)性地建立一體式空心鑄鋁副車架分層級設(shè)計優(yōu)化方法�����。首先��,建立副車架模型并定義局部坐標(biāo)系下的靜剛度計算方法,并根據(jù)K&C 性能指標(biāo)修正靜剛度性能目標(biāo)�����,為副車架多學(xué)科性能優(yōu)化打下科學(xué)的基礎(chǔ)����;其次�����,基于模態(tài)和靜剛度等全局性能開展拓?fù)鋬?yōu)化設(shè)計主體結(jié)構(gòu)��,進而通過局部區(qū)域加強完成變壁厚設(shè)計;經(jīng)過多層級拓?fù)鋬?yōu)化可以在滿足各學(xué)科性能要求����、同時實現(xiàn)副車架最大限度的輕量化。
1 ����、 副車架靜剛度計算方法
1.1 計算模型及邊界條件
副車架作為電動汽車多級隔振的重要一級�����,概念設(shè)計各硬點及名稱如圖1 所示����,其與車身往往通過懸置柔性連接。以圖2 所示的副車架前�����、后懸置點為例闡述柔性連接建模方法:創(chuàng)建兩個串聯(lián)的零長度CBUSH 單元��,一個用于模擬車身安裝點剛度����,另一個用于模擬副車架懸置剛度����,并約束車身端耦合點1~6 自由度。為便于編程�����,前上控制臂簡寫為FUCA�����,前下控制板簡寫為FLCA�����,后上控制臂簡寫為RUCA����,后下控制臂簡寫為RLCA,前束臂簡寫為SCA��。
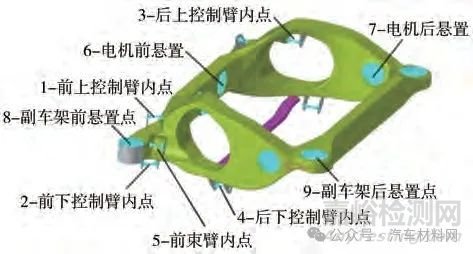
圖1 副車架基準(zhǔn)有限元模型及硬點示意圖
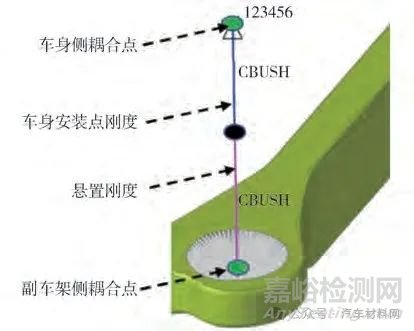
圖2 副車架與車身柔性連接建模示意圖
1.2 加載及靜剛度計算方法
現(xiàn)有分析方法采用在懸架控制臂內(nèi)側(cè)硬點位置分別沿著整車坐標(biāo)系 X、Y��、Z 方向進行加載[7],這無法準(zhǔn)確關(guān)聯(lián)靜剛度與關(guān)注的行駛性能運動特征�����。懸架控制臂運動受力方向與整車坐標(biāo)系坐標(biāo)軸往往存在一定夾角����,為更準(zhǔn)確表征控制臂運動及受力特征��,基于局部坐標(biāo)系進行分析加載和測量�����,局部坐標(biāo)系定義如下:控制臂的軸向定義為局部坐標(biāo)系Y 向,為主方向�����,控制臂襯套軸向為X 向����,局部坐標(biāo)系的Z 向可根據(jù)右手定則獲取且方向朝上�����。加載定義:沿著局部坐標(biāo)系X、Y��、Z向加載1 000 N載荷�����。
按照上述靜剛度計算新方法��,對約束狀態(tài)的副車架進行兩次剛度分析��,第1 次對柔性副車架分析��,剛度記為Ktotal;第2 次分析剛性副車架(在柔性副車架基礎(chǔ)上將材料彈性模量放大1 000 倍等效)����,剛度記為Krigid�����。綜合兩次剛度分析結(jié)果��,通過消除副車架與車身柔性連接的影響�����,定義副車架靜剛度K�����。
式中:Ktotal = F/Uflex�����;Krigid = F/Urigid;Uflex��、Urigid 分別為柔性副車架模型����、剛性體副車架模型同一加載點的位移��。
2 ��、 基于K&C性能的靜剛度目標(biāo)修正
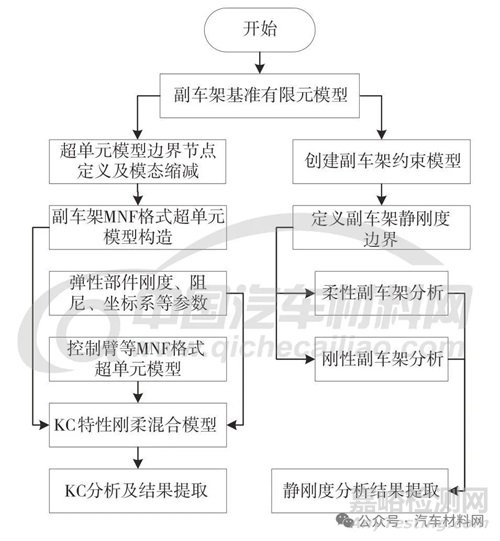
本文建立融合多學(xué)科工況的仿真流程��,見圖3��?�;谕挥邢拊P徒Y(jié)構(gòu)參數(shù),打通靜剛度性能與運動學(xué)K&C 性能兩個學(xué)科之間的關(guān)聯(lián)關(guān)系����。將尚未建立車身柔性連接的副車架作為基準(zhǔn)有限元模型(參考圖1),對副車架與車身的連接進行等效����,建立副車架約束模型�����,進行靜剛度分析�����;將副車架基準(zhǔn)有限元模型����、各控制臂有限元模型轉(zhuǎn)化為超單元模型�����,進一步地����,基于超單元模型建立高精度K&C 模型并進行仿真分析����?����?梢詫崿F(xiàn)副車架靜剛度分析�����、超單元模型縮減分析����、K&C 性能分析3 種工況的并行仿真分析�����,并能自驅(qū)動多樣本迭代計算��。
圖3 靜剛度與K&C的并行仿真流程示意圖
其中�����,高精度剛?cè)峄旌夏P蜆?gòu)建及K&C 仿真分析方法如下:采用Craig-Bampton[9-10]將副車架����、控制臂�����、轉(zhuǎn)向節(jié)等有限元模型縮減為MNF 格式超單元模型����;基于Adams軟件輸入各彈性部件各方向剛度����、阻尼等連接信息,結(jié)合MNF 模型建立運動學(xué)關(guān)系�����,完成懸架K&C 特性分析模型建立,規(guī)避了傳統(tǒng)簡化建模方法無法準(zhǔn)確得到副車架等部件剛度�����、慣量參數(shù)的弊端����;進一步地��,編制批處理命令調(diào)用Adams對高精度分析模型自動求解��,并將仿真結(jié)果轉(zhuǎn)化為可編輯的文本文件格式。
2.1 執(zhí)行實驗設(shè)計
根據(jù)懸架硬點和布置空間��,借助一體式空心鑄鋁副車架的概念設(shè)計數(shù)據(jù)(見圖1)�����,采用本文提出的加載和計算方法完成靜剛度分析,采用高精度剛?cè)峄旌夏P屯瓿蒏&C 仿真分析����。以副車架每個特征面厚度為設(shè)計變量(對稱面設(shè)定共用一個設(shè)計變量),參考工藝能力定義設(shè)計變量范圍為4~9 mm����,利用最優(yōu)拉丁超立方設(shè)計的方法完成200 個樣本點的生成�����,得到設(shè)計變量與靜剛度性能、K&C 性能的實驗設(shè)計矩陣表��,如表1所示����。
表1 實驗設(shè)計矩陣表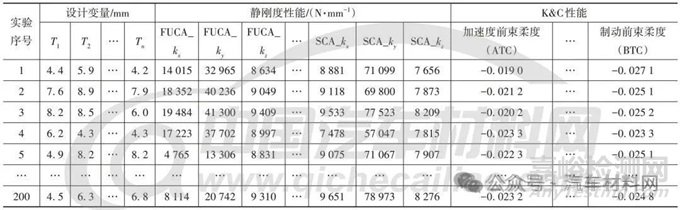
2.2 構(gòu)造性能間的組合代理模型
代理模型的一般數(shù)學(xué)模型可表示如下[11]:

式中:f(x)為真實模型;f?(x)為代理模型�����;ε(x)為近似誤差��。
單一代理模型無法對所有優(yōu)化問題都有較強的預(yù)測能力[12]��,而組合代理模型具有更穩(wěn)定的近似能力[13]�����。一般而言,預(yù)測精度越高對應(yīng)的單一代理模型權(quán)系數(shù)越大��,本文選取精度較高的單一代理模型參與組合代理模型構(gòu)造�����,利用預(yù)測平方和(prediction sum of squares�����,PRESS)誤差評價準(zhǔn)則計算權(quán)重系數(shù)����,建立PWS 組合代理模型(PRESS weighted surrogate��, PWS):

式中:m為參與構(gòu)造組合代理模型f?EN(x)的單一代理
式中:Ek 表示第k 個單一模型的預(yù)測平方和��;Eavg 表示所有單一模型的預(yù)測平方和均值�����;經(jīng)過試驗[14]�����,推薦參數(shù)值α = 0.05,β = -1����。
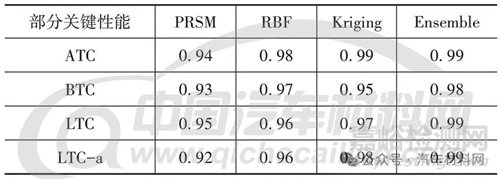
代理模型常用來逼近設(shè)計變量與性能指標(biāo)之間的真實映射關(guān)系�����,而本文研究的重點是靜剛度性能與K&C 性能之間的關(guān)系����,進一步對表1 的實驗設(shè)計矩陣進行轉(zhuǎn)換����,將靜剛度性能指標(biāo)轉(zhuǎn)換為設(shè)計變量����,K&C 性能作為性能指標(biāo)。根據(jù)全局誤差評估指標(biāo)R2(R2 越接近1 精度越高)�����,從12 種常用代理模型中選出精度較大的PRSM��、RBF、Kriging 模型構(gòu)造組合代理模型Ensemble����。精度對比結(jié)果見表2(其中LTC、LTC-a 分別為側(cè)向力����、反側(cè)向力柔度)��,組合代理模型綜合近似能力相對更優(yōu)��。
表2 代理模型精度對比
結(jié)合具體車型K&C 性能開發(fā)需求����,在懸架硬點設(shè)計凍結(jié)前提下�����,篩選��、識別需要通過副車架提升的K&C 性能����,篩選原則:(1)不滿足目標(biāo)值要求的K&C性能��;(2)與副車架剛度相關(guān)性較為顯著的K&C 性能����。識別結(jié)果:加速前束柔度(ACC toe compliance����,ATC)尚未滿足性能目標(biāo)[-0.02,-0.005]下限要求����,且與副車架剛度相關(guān)性較為顯著(相關(guān)性系數(shù)>0.4);制動前束柔度(brake boe compliance����, BTC)、側(cè)向力前束柔度(leteral toe compliance��, LTC)�����;反向側(cè)向力前束柔度(letaral toe compliance anti��, LTC-a)與副車架剛度相關(guān)性較為顯著,但性能均符合目標(biāo)要求�����;故以ATC 為重點優(yōu)化對象,其他K&C 性能作為性能約束�����。
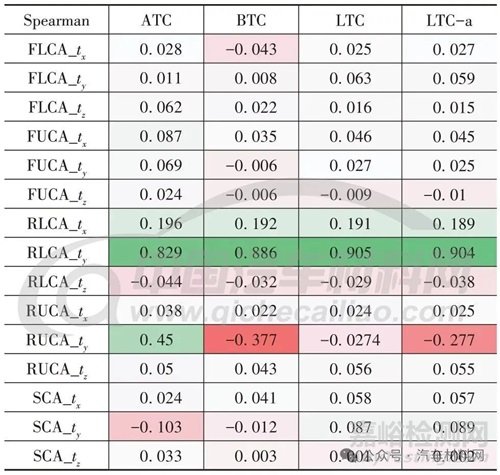
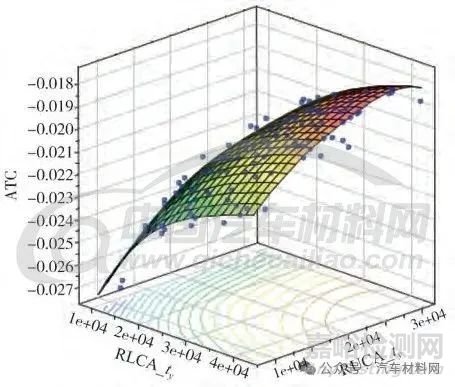
基于Spearman 相關(guān)性系數(shù)統(tǒng)計結(jié)果見表3,發(fā)現(xiàn)5個控制臂中的后下控制臂Y向剛度(RLCA_ty)和后上控制臂Y 向剛度(RUCA_ty)對ATC 性能影響較為顯著��,基于組合代理模型提取顯著設(shè)計變量與關(guān)注性能的映射關(guān)系見圖4��,可以預(yù)測��,增加后下控制臂Y 向、后上控制臂Y 向靜剛度�����,能夠提升前束加速俯仰性能�����。
表3 K&C性能與靜剛度的相關(guān)系數(shù)
圖4 顯著設(shè)計變量與關(guān)注性能映射關(guān)系圖
2.3 靜剛度目標(biāo)修正
本文結(jié)合性能指標(biāo)特征����,采用自適應(yīng)差分進化算法(self-adaptive differential evolution��,SaDE)��,以副車架靜剛度RLCA_ty����、RUCA_ty 為設(shè)計變量����,以K&C 性能為約束和優(yōu)化目標(biāo)進行求解����,其表達式如下:
式中:pi 為K&C 特性中第i 個性能;piL��、piH 分別為第i個性能要求的上下限值����;ti 為第i 個性能的目標(biāo)值,對于ATC性能取目標(biāo)值的中位數(shù)����;twi為權(quán)重系數(shù)����。
優(yōu)化迭代歷程的氣泡圖見圖5����,可以發(fā)現(xiàn)��,為滿足所有K&C 性能需求�����,需要重點提升RLCA_ty、RUCA_ty兩個性能(藍(lán)色樣本為可行方案)��。由圖5也可以看出����,后下控制臂Y 向剛度的上限值較后上控制臂Y 向剛度上限值高33%�����,且后下控制臂附近存在底部加強梁結(jié)構(gòu)����,性能提升潛力更大�����,綜合副車架的初始結(jié)構(gòu)設(shè)計的靜剛度和K&C 性能關(guān)聯(lián)的結(jié)果對靜剛度經(jīng)驗值進行目標(biāo)修正,見表4��,后上����、后下控制臂Y 向靜剛度值需要提升不低于13.6%��、31.8%��。
表4 控制臂主方向靜剛度性能目標(biāo)修正

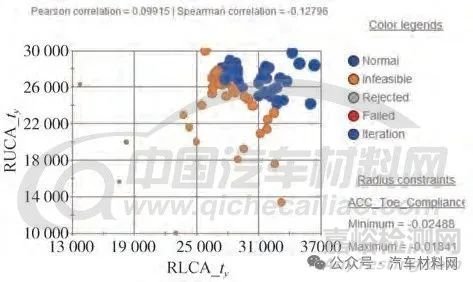
圖5 優(yōu)化迭代氣泡圖
3 ��、 副車架結(jié)構(gòu)多層級拓?fù)鋬?yōu)化
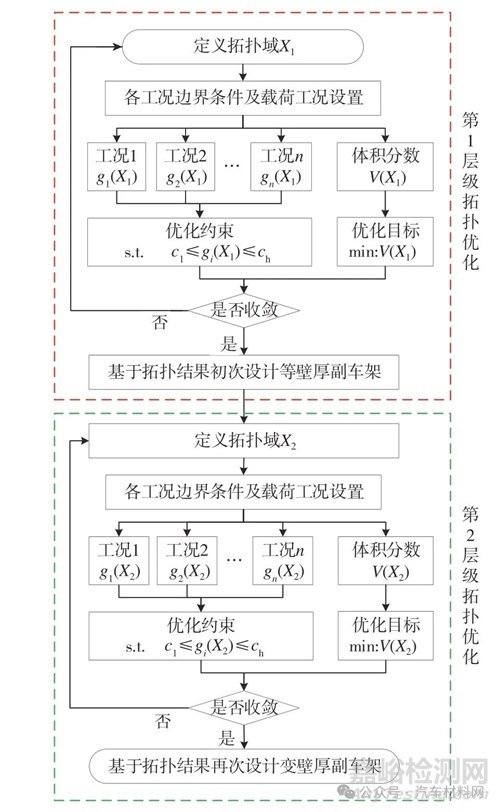
靜動態(tài)多工況拓?fù)鋬?yōu)化設(shè)計多采用建立綜合目標(biāo)函數(shù)并確定子目標(biāo)權(quán)重系數(shù)的折衷規(guī)劃法,本質(zhì)上是將多目標(biāo)優(yōu)化問題轉(zhuǎn)化為單目標(biāo)優(yōu)化問題[15]�����。針對各工況性能目標(biāo)明確的優(yōu)化�����,將多工況性能目標(biāo)優(yōu)化問題轉(zhuǎn)化為以多工況性能目標(biāo)為約束����、最小化拓?fù)溆蝮w積分?jǐn)?shù)的優(yōu)化問題[16]�����,可獲得較為準(zhǔn)確的結(jié)構(gòu)路徑����。本文結(jié)合一體式空心鑄鋁副車架的工藝特征����,提出基于多性能約束的多層級拓?fù)鋬?yōu)化方法,見圖6�����,其中V(X)表示體積分?jǐn)?shù)�����,gi(X)表示第i個工況的性能�����,本文約束工況gi(X)包括靜剛度����、模態(tài)��、動剛度性能��,cl為性能目標(biāo)下限值��,ch為性能目標(biāo)上限值����。
圖6 基于多性能約束的多層級拓?fù)鋬?yōu)化方法
多層級設(shè)計優(yōu)化思路為:第1 層級拓?fù)湟愿拍羁尚性O(shè)計空間X1 為優(yōu)化對象��,識別關(guān)鍵傳力路徑����,完成壁厚為T1 的副車架設(shè)計�����;第2 層級拓?fù)?�,在?層級設(shè)計基礎(chǔ)上��,在內(nèi)壁區(qū)域增加設(shè)計空間X2����,對應(yīng)的厚度為T2�����,以設(shè)計空間X2 為優(yōu)化對象��,識別對性能靈敏度區(qū)域�����,完成變壁厚具體結(jié)構(gòu)設(shè)計��。其中,T1為工藝可行的最小厚度值����,T1+T2為工藝可行的最大厚度值。
拓?fù)鋬?yōu)化采用SIMP方法�����,拓?fù)溆?X 被離散為一定數(shù)量的單元�����,將密度作為設(shè)計變量賦予每個單元��,利用數(shù)學(xué)規(guī)劃法決定單元密度�����,1 表示有材料�����,0 表示材料完全刪除����,材料插值模型表達如下[17]:
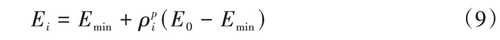
式中:Ei 為第i 個單元插值后的彈性模量��;E0�����、Emin 分別為單元初始定義的彈性模量和最小彈性模量��;ρi為第 i 個單元的相對密度����,ρi ∈[0����,1]��; p 為懲罰因子��。本文定義實體單元懲罰因子p = 3�����,Emin/E0 =0.01�����。
3.1 第1層級拓?fù)鋬?yōu)化
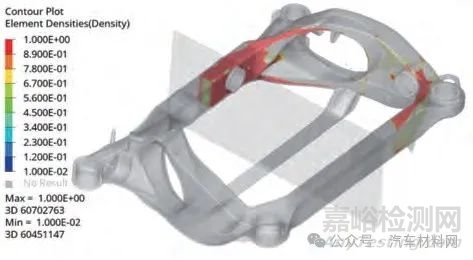
拓?fù)溆騒1 定義為整體設(shè)計空間減去懸架運動包絡(luò)區(qū)域及相關(guān)件(電驅(qū)系統(tǒng)�����、車身底護板����、車身縱梁等)布置區(qū)域后的概念可行設(shè)計空間����。拓?fù)溆騒1劃分為實體網(wǎng)格,開展第1 層級多模型拓?fù)鋬?yōu)化�����,拓?fù)鋬?yōu)化結(jié)果如圖7����。
圖7 第1層級拓?fù)鋬?yōu)化1/2截面圖示意
根據(jù)拓?fù)鋬?yōu)化結(jié)果設(shè)計副車架主體結(jié)構(gòu)框架��,設(shè)計原則定義如下:(1)根據(jù)拓?fù)浣Y(jié)果的關(guān)鍵傳力路徑(單元密度接近1 的單元)����,解讀副車架各區(qū)域的截面特征及過渡設(shè)計��,確定副車架主體結(jié)構(gòu)��;(2)副車架初始壁厚統(tǒng)一采用工藝可實施的最小厚度��?���;谕?fù)浣Y(jié)果完成等壁厚副車架的初次設(shè)計,見圖8�����,已具備副車架工程設(shè)計的雛形�����,相較于圖1 的概念設(shè)計方案����,優(yōu)化后的副車架下橫梁沿+X 向后移����,且與副車架主體呈一體化鑄造成型,后下控制臂接附點嵌入加強梁端部��,對后下控制臂位置靜剛度提升更為直接����。

圖8 等壁厚設(shè)計方案示意圖
3.2 第2層級拓?fù)鋬?yōu)化
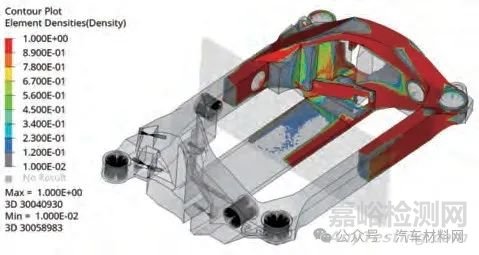
副車架初次工程設(shè)計方案采用工藝可實施最小厚度��,此時圖8 的等壁厚結(jié)構(gòu)設(shè)計方案未能充分體現(xiàn)圖7 拓?fù)鋬?yōu)化的理想效果��。對圖8 的設(shè)計數(shù)據(jù)進行仿真分析����,發(fā)現(xiàn)模態(tài)及部分剛度性能尚未達標(biāo)��,為滿足所有性能需求����,有必要進一步借助拓?fù)鋬?yōu)化識別性能靈敏的結(jié)構(gòu)區(qū)域,通過對靈敏區(qū)域加強設(shè)計�����,形成變厚度方案��。將副車架初次設(shè)計方案作為非設(shè)計域��,在梁系內(nèi)側(cè)構(gòu)造的封閉空間定義為拓?fù)溆騒2�����,進行第2層級拓?fù)鋬?yōu)化��,優(yōu)化結(jié)果如圖9所示��。
圖9 第2層級拓?fù)鋬?yōu)化1/2截面圖示意
可以發(fā)現(xiàn):與第1 層級優(yōu)化特征不同,第2 層級拓?fù)鋬?yōu)化的特征是局部區(qū)域材料聚集����,說明此區(qū)域?qū)π阅莒`敏度較高��,需要在空心梁壁對應(yīng)區(qū)域的內(nèi)側(cè)或外側(cè)加強����,改進為變壁厚的再次設(shè)計方案����,并對方案進行性能驗證�����。本文副車架前橫梁中部區(qū)域?qū)π阅茏铎`敏����,高靈敏度區(qū)域的單元密度也均接近1,同時為降低工藝難度�����,將圖9 中材料聚集區(qū)域均勻增加壁厚�����,前橫梁底部區(qū)域變厚度設(shè)計如圖10 所示��,最大厚度和最小厚度之間的過渡區(qū)采用倒角平滑過渡����,最大厚度采用工藝可行最大厚度6 mm����,最小厚度采用工藝可行最小厚度4 mm,副車架結(jié)構(gòu)����、厚度為左右對稱設(shè)計����。
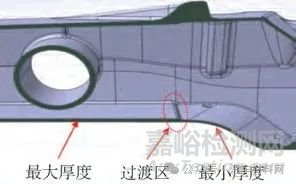
圖10 變壁厚設(shè)計方案示意圖
3.3 副車架優(yōu)化方案驗證
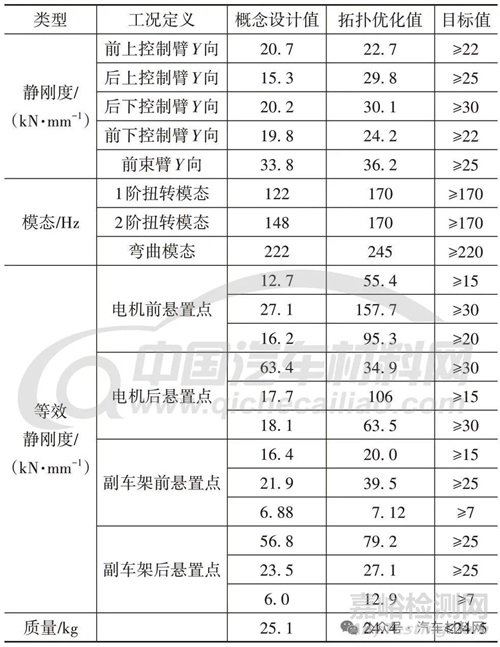
參考第2 層級拓?fù)鋬?yōu)化結(jié)果�����,對副車架進行工程化設(shè)計�����,仿真驗證發(fā)現(xiàn)靜態(tài)工況�����、模態(tài)工況��、動剛度工況等相關(guān)全局性能全部達標(biāo)����,與概念設(shè)計方案性能對比見表5。
表5 關(guān)鍵性能對比
對比結(jié)構(gòu)設(shè)計演變過程和性能變化可以發(fā)現(xiàn):拓?fù)鋬?yōu)化方案的各項性能指標(biāo)均得到顯著提升并減質(zhì)量0.7 kg�����;2階扭轉(zhuǎn)模態(tài)是目標(biāo)體系下副車架結(jié)構(gòu)的決定因素�����,優(yōu)化后性能分別提升39.3%����、14.9%,達成模態(tài)指標(biāo)需要強化副車架前橫梁結(jié)構(gòu)設(shè)計�����,而電機前懸置點等效靜剛度遠(yuǎn)超目標(biāo)值說明其對前橫梁設(shè)計影響較?���。煌瑫r�����,第1 層級拓?fù)鋬?yōu)化使下橫梁后移��,后下控制臂內(nèi)嵌于下橫梁端頭的設(shè)計����,也促進后下控制臂Y向性能大幅提升。
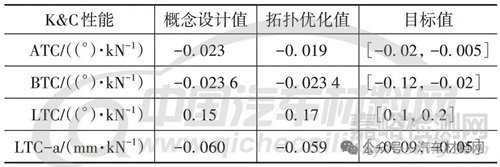
將副車架工程化方案有限元模型超單元轉(zhuǎn)化執(zhí)行K&C 特性分析�����,見表6。由表可見:K&C 各性能�����,特別是與副車架剛度相關(guān)性較為顯著的各項性能均滿足目標(biāo)�����;ATC 性能得到改善����,由不達標(biāo)轉(zhuǎn)化為滿足目標(biāo)要求。這也在一定程度上說明根據(jù)K&C 性能對靜剛度目標(biāo)修正�����,并通過優(yōu)化靜剛度改善K&C性能的方法是有效的����。
表6 與副車架剛度顯著相關(guān)的K&C性能對比
4 ����、 結(jié)論
(1)本文改進靜剛度加載方法�����,提出局部坐標(biāo)系下的靜剛度計算新方法��,基于有限元模型結(jié)構(gòu)參數(shù)����,打通靜剛度性能與運動學(xué)K&C 性能兩個學(xué)科之間的關(guān)系����?����;诮M合代理模型��,挖掘靜剛度性能與K&C 性能之間的耦合關(guān)聯(lián)規(guī)律�����,修正靜剛度性能目標(biāo)��,可為工程中K&C 性能提升及副車架靜剛度性能指標(biāo)制定提供參考�����。
(2)提出鑄鋁副車架多層級設(shè)計優(yōu)化思路�����,并進行副車架多層級拓?fù)鋬?yōu)化�����,開展第1 層級拓?fù)鋬?yōu)化完成等壁厚主體結(jié)構(gòu)設(shè)計,開展第2 層級拓?fù)鋬?yōu)化加強局部區(qū)域完成變壁厚工程化設(shè)計����。結(jié)果表明,優(yōu)化副車架在滿足多學(xué)科全局性能指標(biāo)的同時實現(xiàn)輕量化��,靜剛度及關(guān)聯(lián)的K&C 性能滿足目標(biāo)����,模態(tài)性能大幅提升。
參考文獻
[ 1 ] FAN W����, YIN L, XU Z��, et al.Two-stage surrogate-based optimization of a vehicle composite subframe with modified fast flexible space-filling designs[J].Mechanics of Advanced Materials and Structures, 2023��, 30(4):724-737.
[ 2 ] NAM J S����, SHIN H W�����, CHOI G J.Durability prediction for automobile aluminum front subframe using nonlinear models in virtual test simulations [J].International Journal of Automotive Technology��, 2014�����, 15(4):593-601.
[ 3 ] MENG X��, SUN Y�����, HE J��, et al.Multi-objective lightweight optimization design of the aluminum alloy front subframe of a vehicle[J].Metals��, 2023�����, 13(4):705.
[ 4 ] OUYANG T����, WU J��, CHEN Q����, et al.Multi-objective combination optimization of automobile subframe dynamic stiffness[C].SAE Paper 2023-01-0005.
[ 5 ] 朱劍峰, 王水瑩��, 林逸��, 等.后副車架拓?fù)鋬?yōu)化概念設(shè)計和智能輕量化方法研究[J].汽車工程����, 2015, 37(12):1471-1476.ZHU Jianfeng��, WANG Shuiying�����, LIN Yi, et al.A study on the methods of concept design with topology optimization and intelligent lightweighting for rear subframe[J].Automotive Engineering��, 2015�����, 37(12):1471-1476.
[ 6 ] 馬芳武�����, 王卓君�����, 楊猛�����, 等.汽車后副車架輕量化概念設(shè)計方法研究[J].汽車工程��, 2021����, 43(5):776-783.MA F W����, WANG Z J��, YANG M�����, et al.Research on lightweight conceptual design method of vehicle rear subframe[J].Automotive Engineering�����, 2021��, 43(5):776-783.
[ 7 ] 廖鶯��,李峰����,李志.概念設(shè)計階段鋁合金后副車架輕量化設(shè)計[J].汽車工程����,2020, 42(12):1737-1743.LIAO Y����, LI F, LI Z.Lightweight design of aluminum rear subframe in conceptual design stage [J].Automotive Engineering����,2020��, 42(12):1737-1743.
[ 8 ] 林佳武����, 李玄霜�����, 陳宗明�����, 等.真空高壓鑄造鋁合金車身后縱梁輕量化設(shè)計[J].汽車工程��, 2020����, 42(3):383-389.LIN J W����, LI X S, CHEN Z M�����, et al.Lightweight design of body rear longitudinal beam of VAHP die-casting aluminum alloy[J].Automotive Engineering��, 2020����, 42(3):383-389.
[ 9 ] WU L �����, TISO P �����, KEULEN F V.Interface reduction with multilevel craig–bampton substructuring for component mode synthesis[J].AIAA Journal�����, 2018�����, 56(5):1-15.
[ 10 ]PRADEEPKUMAR S �����, NAGARAJ P.Dynamic substructuring method for vibration analysis of complex structures[J].Journal of Vibration Engineering & Technologies����, 2022(1):10.
[ 11 ]龍騰,劉建��,WANG G Gary�����,等.基于計算試驗設(shè)計與代理模型的飛行器近似優(yōu)化策略探討[J].機械工程學(xué)報����,2016��,52(14):79-105.LONG T����, LIU J����, WANG G Gary, et al.Discuss on approximate optimization strategies using design of computer experiments and metamodels for flight vehicle design[J].Journal of Mechanical Engineering����, 2016�����, 52(14):79-105.
[ 12 ]童水光, 何順�����, 童哲銘����, 等.基于組合近似模型的輕量化設(shè)計方法[J].中國機械工程��, 2020�����, 31(11):1337.TONG S G����, HE S, TONG Z M����, et al.Lightweight design method based on combined approximation model [J].China Mechanical Engineering��, 2020, 31(11):1337.
[ 13 ]VIANA F A C��, HAFTKA R T��, STEFFEN V.Multiple surrogates:how cross-validation errors can help us to obtain the best predictor[J].Structural and Multidisciplinary Optimization����,2009��, 39(4):439-457.
[ 14 ]GOEL T�����, HAFTKA R T����, SHYY W����, et al.Ensemble of surrogates [J].Structural and Multidisciplinary Optimization�����, 2007,33(3):199-216.
[ 15 ]張志飛��, 陳仁�����, 徐中明����,等.面向多目標(biāo)的汽車懸架控制臂拓?fù)鋬?yōu)化研究[J].機械工程學(xué)報�����, 2017��, 53(4):114-121.ZHANG Z F����, CHEN R��, XU Z M��, et al.Research on multi-objective topology optimization of vehicle suspension control arm [J].Journal of Mechanical Engineering, 2017��, 53(4):114-121.
[ 16 ]占金青����, 彭怡平����, 劉敏, 等.基于多性能約束的連續(xù)體結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計[J].計算機集成制造系統(tǒng)����, 2022, 28(6):1746-1754.ZHAN J Q����, PENG Y P, LIU M��, et al.Topology optimization of continuum structures with multiple performance constraints [J].Computer Integrated Manufacturing Systems�����, 2022����, 28(6):1746-1754.
[ 17 ]廉睿超����, 敬石開��, 李營����, 等.考慮最小尺寸精確控制的SIMP和MMC 混合拓?fù)鋬?yōu)化方法[J].力學(xué)學(xué)報, 2022��, 54(12):3524-3537.LIAN R C��, JING S K����, LI Y, et al.A hybrid topology optimization method of SIMP and MMC considering precise control of minimum size[J].Chinese Journal of Theoretical and Applied Mechanics��, 2022�����, 54(12):3524-3537.