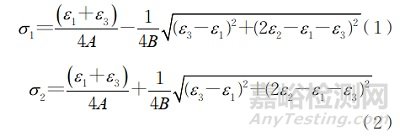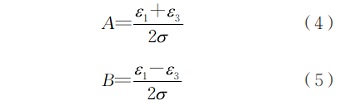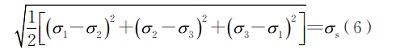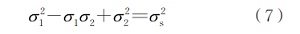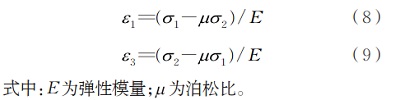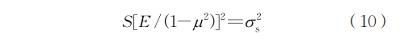5083鋁合金是典型的Al-Mg系合金�,具有優(yōu)異的比強度、耐腐蝕性及可焊性�,已成為船舶制造領域不可或缺的結構材料,尤其在游艇�、快艇及軌道車輛廂體等高端裝備中占據(jù)主導地位。然而�,該材料具有較高的線膨脹系數(shù)(約2.36×10−4℃−1)和顯著的凝固收縮特性(約5% 的體積收縮率)�,這導致其在焊接過程中易形成高達母材屈服強度60% 的殘余應力場�,并伴隨熱裂紋的萌生與擴展,嚴重削弱了結構的疲勞壽命與尺寸穩(wěn)定性�。因此,精準表征焊接殘余應力的分布特征�、揭示其演化規(guī)律,成為提升5083鋁合金焊接構件可靠性的核心課題�。
殘余應力檢測技術經(jīng)過多年發(fā)展�,已形成多元化檢測體系,主要包括盲孔法�、X 射線衍射法、中子衍射法�、超聲法及磁性法。其中�,盲孔法憑借微破壞性、操作便捷性及成本可控性等優(yōu)勢�,逐漸發(fā)展成為殘余應力測試的主流方法。盲孔釋放法的理論框架于1934年首次提出�,后期經(jīng)一些學者的完善,建立了標準化測試流程�,并實現(xiàn)了應變釋放系數(shù)A、B的實驗室標定�。需特別指出的是,殘余應力測量精度直接取決于應變釋放系數(shù)A�、B的準確性�,二者的誤差會導致應力計算結果產(chǎn)生系統(tǒng)性偏差�。馬雯波等對Q345R鋼的應變釋放系數(shù)進行研究后發(fā)現(xiàn),當應力小于等于0.6倍屈服強度時�,使用彈性段標定的應變釋放系數(shù)計算應力的相對誤差低于4%;而當應力達到0.9倍屈服強度時�,殘余應力誤差可達45%。左善超等對Q235鋼的應變釋放系數(shù)研究結果表明�,由應變釋放系數(shù)引起的殘余應力誤差最大可達83%。譚明鶴等與劉曉紅等分別對921A鋼與16Mn鋼的應變釋放系數(shù)進行研究�,也得出了相似結論�。在焊接殘余應力檢測領域,盡管已有大量針對盲孔法釋放系數(shù)的標定與修正研究�,但現(xiàn)有成果多集中于鋼材體系。5083鋁合金的高殘余應力區(qū)應變釋放特性的系統(tǒng)性研究較少�,需要構建適用于該材料的標定與修正方法體系。
筆者以5083鋁合金為研究對象�,探究了不同應力條件下的應變釋放系數(shù);同時�,鑒于高應力塑性變形的影響,對測試的應變釋放系數(shù)進行了修正�。該研究成果可為5083 鋁合金焊接結構的殘余應力精準評估提供理論依據(jù),也能為其他金屬及其合金材料的應變釋放系數(shù)標定提供參考�。
01|盲孔法測試殘余應力的基本原理
盲孔法作為一種經(jīng)典的殘余應力場無損檢測手段,其理論基礎源于材料力學中的應力松弛效應�。當材料內(nèi)部存在殘余應力場時�,通過在其表面特定位置鉆削直徑為d�、深度為h的小盲孔,局部區(qū)域的殘余應力會因孔壁材料的移除而被釋放�,這會引發(fā)周圍應力場的再平衡,并伴隨幾何應變場的改變�。此過程中釋放的應變與原始殘余應力呈正相關關系,可通過高靈敏度應變花精確測量�,進而反演初始應力狀態(tài),其應力計算公式如式(1)~(3)所示�。
A、B主要與待測材料的彈性模量�、泊松比、鉆孔直徑及所用應變花的尺寸有關�。通孔的A、B可通過柯西理論解計算得出�;由于盲孔的應力集中系數(shù)與通孔不同,其 A�、B通常通過標定獲得。應變釋放系數(shù)通常通過拉伸試驗機進行標定:對已貼應變花的標定試樣施加單向拉應力σ�,使其中一個電阻應變片平行于該外力方向,此時最大主應力σ1即為σ�,最小主應力σ2為0。將其代入殘余應力計算公式(1)與(2)�,即可得到應變釋放系數(shù)的標定公式(4)、(5)�;根據(jù)1 號�、3號應變片所采集的釋放應變ε1�、ε3,便可求得應變釋放系數(shù)A�、B。
02|應變釋放系數(shù)的標定
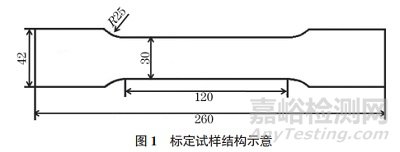
選用5083鋁合金作為試驗材料�,試樣結構(厚度為7.5mm)如圖1所示。為確保標定試樣無初始應力�,需對其進行去應力處理,具體工藝參數(shù)為:采用液氮深冷處理工藝(-196℃�,2h),隨后空冷至室溫�。為評估去應力處理效果,使用X射線應力儀對試樣表面進行隨機五點殘余應力測試�。測試結果顯示�,殘余應力分別為4.3,5.8�,1.8,3.5�,-3.2MPa。經(jīng)統(tǒng)計分析得出�,平均殘余應力為2.4MPa,標準差為3.5MPa�,表明試樣初始應力已得到有效消除。
03|力學性能試驗
為確定標定試驗的加載應力范圍�,需獲取材料的基礎力學參數(shù)�。采用萬能力學試驗機對兩組5083鋁合金試樣進行拉伸試驗�,其力學性能測試結果如表1所示。
標定用的設備主要有萬能力學試驗機�、動態(tài)電阻應變儀、鉆孔裝置�、電阻應變片。具體的標定過程如下:①將貼好應變片的標定試樣安裝在萬能力學試驗機上�,將各應變片示數(shù)調(diào)零,加載至預定載荷�,記錄各個載荷下1號、3號應變片所采集的示數(shù)ε10�、ε30;②將試樣從萬能力學試驗機上取下�,采用鉆孔裝置實施定位鉆孔,鉆孔參數(shù)設定為直徑1.5mm�、深度2mm;③將鉆孔后的試樣重新安裝在萬能力學試驗機上并完成應變片二次歸零�,重復相同載荷加載程序,記錄各個載荷下1號�、3號應變片所采集的示數(shù)ε11、ε31�;④將鉆孔后各應變片的示數(shù)減去鉆孔前的示數(shù),即可得到在各自載荷下引起的釋放應變ε1�、ε3,將其代入式(4)與式(5),即可計算出應變釋放系數(shù)A�、B。
04|結果與分析
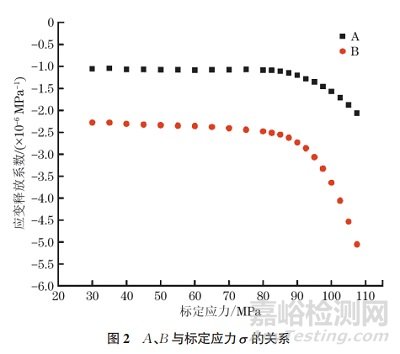
A�、B與標定應力σ 的關系如圖2所示。由圖2可知:當標定應力不大于75MPa(約0.6σs�,σs為屈服強度)時,隨著標定應力的增大�,A、B整體呈略有減小的趨勢�;當標定應力大于75MPa時,隨著標定應力的增大�,A、B開始急劇減小�。根據(jù)彈性力學理論,在單向拉伸應力狀態(tài)下�,圓孔的應力集中系數(shù)為3,即當標定應力σ大于σs/3時�,由于應力集中作用,圓孔邊緣的應力狀態(tài)已達到屈服應力σs�,圓孔邊緣材料開始發(fā)生塑性變形�,此時A、B逐漸減小�。根據(jù)GB/T 31310—2014《金屬材料 殘余應力測定 鉆孔應變法》標準,當殘余應力不超過屈服強度的60%時�,孔邊緣材料的變形仍可近似認為是彈性變形,因此A、B不會明顯減?。划敋堄鄳Υ笥谇姸鹊?0%時�,孔邊緣材料已發(fā)生較大塑性變形,此時A�、B受塑性變形影響而明顯減小。這表明�,彈性理論已無法準確描述和預測孔邊緣發(fā)生塑性變形時的應變釋放規(guī)律。
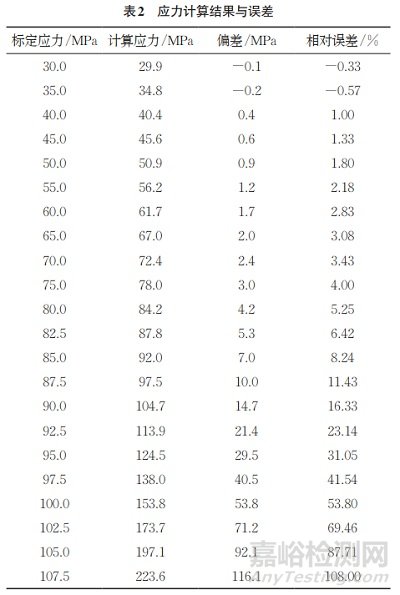
根據(jù)以上標定結果�,分別求得5083 鋁合金在完全彈性段(σ<σs/3)的應變釋放系數(shù)平均值:A的計算結果為-1.057 96×10−6MPa−1,B的計算結果為-2.287×10−6MPa−1�。采用該應變釋放系數(shù)A、B進行殘余應力計算�,詳細結果如表2所示。
由表2可知:當應力不大于75MPa(約0.6σs)時�,盡管隨著應力的增大,相對誤差逐漸增大�,但仍未超過4%;當應力大于75MPa時�,相對誤差隨應力增大而迅速增大,在應力為107.5MPa(約 0.9σs)時�,相對誤差已達到108%,這表明此時彈性理論完全不再適用�,必須考慮塑性變形的影響。因此�,當殘余應力大于屈服強度的60%時,需對A、B進行修正�,以消除孔邊緣塑性變形對應力測試精度的影響。
根據(jù)第四強度理論�,無論是單向應力狀態(tài)還是復雜應力狀態(tài),只要形狀改變比能達到材料單向拉伸屈服時的極限值�,就會導致材料發(fā)生塑性屈服,并可用式(6)來表示�。
在平面應力狀態(tài)下,σ3為零�,因此,上式可化簡為
根據(jù)廣義胡克定律
將式(8)�、(9)代入式(7)的左側可得
由式(10)可知:E、μ�、σs均為與材料相關的常量,當形狀改變比能參量S達到一定數(shù)值后�,材料就會發(fā)生塑性屈服。
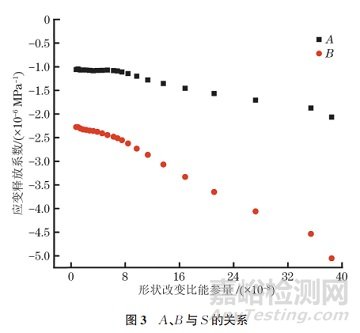
圖3為A�、B與S的關系。由圖3可知:當S較小時�,材料各處均處于彈性變形狀態(tài),A�、B與S的關系不大;當S增大到一定水平(S=53735.18)時�,盲孔邊緣開始發(fā)生明顯的塑性變形�,A、B隨著S的增大呈近似線性下降的趨勢。據(jù)此�,可通過線性擬合的方式,利用S對A�、B進行分段修正,修正公式如式(12)�、(13)所示。
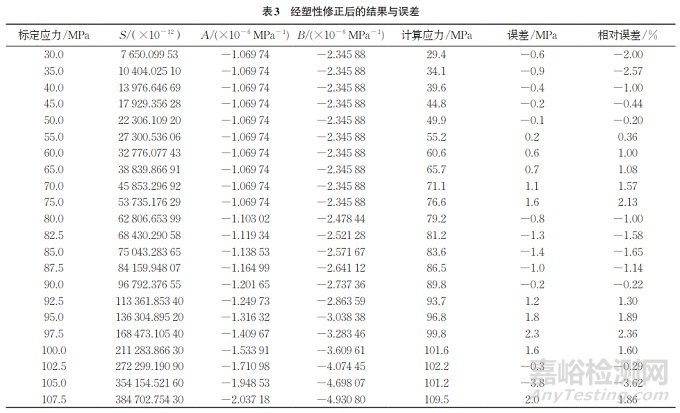
采用修正后的A�、B進行殘余應力計算,結果如表3所示�。由表3可知:在整個標定應力范圍內(nèi),計算應力誤差絕對值不超過3.8MPa�,相對誤差絕對值不超過3.62%;與未修正前的計算結果(最大可達108%)相比�,測試精度顯著提高。
05|結論
(1)當應力不大于0.6σs時�,圓孔邊緣材料仍可近似認為處于彈性應變階段,應變釋放系數(shù)A�、B變化不大;當應力超過0.6σs時�,圓孔邊緣材料已經(jīng)發(fā)生了塑性變形,應變釋放系數(shù)A�、B隨應力的增大顯著減小,彈性理論已無法準確描述與預測孔邊緣變形條件下的應變釋放規(guī)律�。
(2)當應力不大于0.6σs 時,使用彈性段標定的A�、B計算應力�,相對誤差小于4%�;當應力大于0.6σs時,相對誤差迅速增大�,最大可達108%,此時該應變釋放系數(shù)不再適用�,必須考慮塑性變形的影響。
(3)采用S對A�、B進行修正后,在整個應力范圍內(nèi)�,相對誤差絕對值不超過3.62%;與未修正前的計算結果相比�,測試精度顯著提高。
(4)研究結果可為其他金屬材料及其合金的應變釋放系數(shù)標定與修正提供參考�。但受限于試樣材料、應變花尺寸�、鉆孔深度及鉆孔直徑的差異,應變釋放系數(shù)標定與修正結果不能直接套用�,需按照文中方法自行標定。