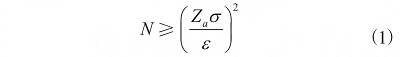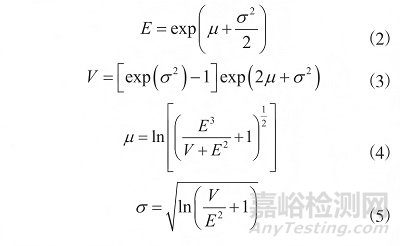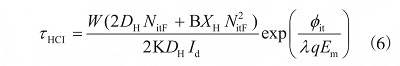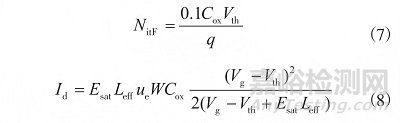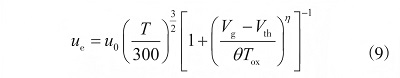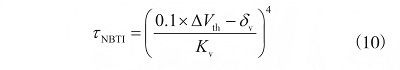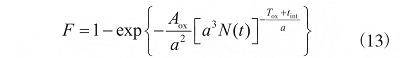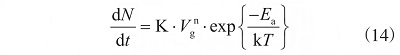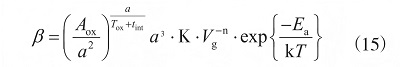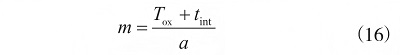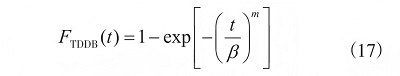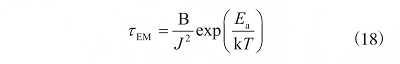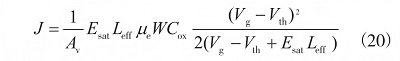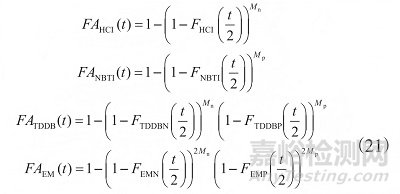摘 要:集成電路器件是產(chǎn)品可靠工作的基礎(chǔ),只有提高集成電路的可靠性�����, 才能確保整個(gè)設(shè)備的可靠性。以理化分析為基礎(chǔ)�����,從本質(zhì)上探究產(chǎn)品的不可靠因素�����,通過(guò)蒙特卡羅仿真方法得出集成電路顯著的失效機(jī)理的失效分布,為集成電路的失效率預(yù)計(jì)提供技術(shù)和方法基礎(chǔ)�����。
關(guān)鍵詞:集成電路�����;蒙特卡洛仿真�����;失效率預(yù)計(jì)
作者:王晉婧�����;牛皓;李睿峰�����;侯巍
作者單位:中國(guó)航天標(biāo)準(zhǔn)化研究所�����;工業(yè)和信息化部電子第五研究所
引 言
集成電路在國(guó)民經(jīng)濟(jì)多個(gè)領(lǐng)域均應(yīng)用廣泛�����,特別是在電子信息技術(shù)中更是不可或缺�����,是信息社會(huì)經(jīng)濟(jì)發(fā)展的基石和動(dòng)力�����。集成電路被廣泛地應(yīng)用于裝備的計(jì)算機(jī)�����、導(dǎo)航設(shè)備�����、通信設(shè)備�����、雷達(dá)�����、制導(dǎo)設(shè)備和電子干擾抑制設(shè)備中�����,是現(xiàn)代裝備技術(shù)的核心和基礎(chǔ)�����。
軍工產(chǎn)品的使用環(huán)境通常都比較惡劣�����,要求集成電路具備高可靠性�����、良好的環(huán)境適應(yīng)能力�����。隨著集成電路在設(shè)備中占比的提升�����,提高集成電路的可靠性�����、降低其失效率�����,才能確保設(shè)備可靠性的提升�����。因此�����,失效率預(yù)計(jì)技術(shù)對(duì)準(zhǔn)確評(píng)估和預(yù)測(cè)集成電路的可靠性具有非常重要的作用。
1 國(guó)內(nèi)外研究現(xiàn)狀
我國(guó)在20世紀(jì)70年代引入美國(guó)可靠性預(yù)計(jì)理論模型�����,并進(jìn)行了大量的失效數(shù)據(jù)收集,在1987年推出了《電子設(shè)備可靠性預(yù)計(jì)手冊(cè)》[1]�����,該手冊(cè)至今已被 4 次更新�����。手冊(cè)中開(kāi)展可靠性預(yù)計(jì)的核心是建立可靠性指標(biāo)同環(huán)境變量�����、系統(tǒng)狀態(tài)變量之間的聯(lián)系�����,根據(jù)產(chǎn)品使用條件的環(huán)境變量與系統(tǒng)狀態(tài)變量來(lái)計(jì)算產(chǎn)品的可靠性[2]�����。該手冊(cè)提供的失效/故障數(shù)據(jù)來(lái)源于現(xiàn)場(chǎng)�����,因此可為可靠性預(yù)計(jì)的準(zhǔn)確性提供數(shù)據(jù)基礎(chǔ)�����。
失效物理是可靠性工程的一個(gè)重要領(lǐng)域�����,也是可靠性技術(shù)發(fā)展的一個(gè)新階段[3]�����。該方法最早由馬里蘭大學(xué)CALCE中心的 Michael Pecht 教授于20世紀(jì) 80 年代提出[4],并逐步應(yīng)用到電子產(chǎn)品的可靠性預(yù)計(jì)中�����。該方法以理化分析為基礎(chǔ),從本質(zhì)上探究產(chǎn)品的不可靠因素,從而為產(chǎn)品的研制�����、生產(chǎn)和使用提供科學(xué)的信息與依據(jù)�����,它是物理學(xué)與可靠性相結(jié)合的新學(xué)科�����。
與《電子設(shè)備可靠性預(yù)計(jì)手冊(cè)》中的方法相比�����,基于失效機(jī)理的可靠性預(yù)計(jì)在國(guó)內(nèi)應(yīng)用還十分有限�����。國(guó)內(nèi)較多研究機(jī)構(gòu)已經(jīng)嘗試?yán)檬C(jī)理的方法對(duì)核心關(guān)鍵集成電路開(kāi)展壽命預(yù)計(jì)�����、薄弱環(huán)節(jié)定位等工作,但工程推廣應(yīng)用還十分有限�����。
2 集成電路失效機(jī)理及失效分布仿真方法
2.1 集成電路失效機(jī)理
集成電路芯片主要的失效機(jī)理包括熱載流子注入(HCI)�����、負(fù)偏壓溫度不穩(wěn)定性(NBTI)�����、與時(shí)間相關(guān)的介質(zhì)擊穿(TDDB)和電遷移(EM)4種,本文在前期研究的理論成果基礎(chǔ)上�����,針對(duì)芯片的4種失效機(jī)理開(kāi)展研究。
2.2 失效分布的蒙特卡羅仿真方法
對(duì)于芯片的各種失效機(jī)理�����,根據(jù)其理化模型�����,通過(guò)蒙特卡羅仿真方法抽樣生成模型參數(shù)不確定性的大量隨機(jī)數(shù)樣本�����,從而仿真求得集成電路的失效分布,并對(duì)失效分布進(jìn)行正態(tài)分布�����、對(duì)數(shù)正態(tài)分布和威布爾分布擬合�����,擬合結(jié)果趨于一條直線則可確定其滿足該分布。具體仿真方法如下�����。
1)樣本數(shù)量
理化模型中不確定參數(shù)創(chuàng)建的樣本量N應(yīng)滿足式(1)�����。
式中:ε為要求的誤差,a為顯著性水平�����,σ為標(biāo)準(zhǔn)差�����,Za為與置信度a相對(duì)應(yīng)的值�����。
本文在仿真中設(shè)定隨機(jī)參數(shù)的標(biāo)準(zhǔn)差σ為0.1�����,仿真結(jié)果誤差ε為0.01�����,顯著性水平a為0.002�����,可計(jì)算得到 Za 為3.092�����。因此�����, 樣本量N最小為9 560.464�����,即仿真的樣本量應(yīng)達(dá)到9561及以上�����。為確保結(jié)果的精確性�����,本文設(shè)置樣本量為10000�����。
2)生成隨機(jī)數(shù)
根據(jù)理化模型確定隨機(jī)參數(shù),生成這些參數(shù)的隨機(jī)數(shù)�����,且隨機(jī)數(shù)應(yīng)符合正態(tài)分布�����。
3)統(tǒng)計(jì)分析
將生成的樣本數(shù)據(jù)代入理化模型中�����,計(jì)算各失效機(jī)理壽命�����,根據(jù)失效閾值獲得失效數(shù)據(jù)�����,統(tǒng)計(jì)所有樣本的期望與方差�����。
4)擬合失效分布
利用擬合失效分布確定壽命的分布類型�����。
5)確定影響壽命的主要因素
當(dāng)影響壽命的參數(shù)不止1個(gè)時(shí),可將各個(gè)影響參數(shù)分別作為單一隨機(jī)變量進(jìn)行蒙特卡羅仿真�����,通過(guò)式(2)和式(3)計(jì)算由該參數(shù)決定的失效分布期望 E 與方差 V�����,再反推分布參數(shù)的均值 μ 和標(biāo)準(zhǔn)差 σ�����,(見(jiàn)式(4)和式(5))�����,由標(biāo)準(zhǔn)差的大小來(lái)確定影響壽命的主要因素�����。
3 集成電路失效機(jī)理的失效分布仿真
3.1 HCI
HCI 導(dǎo)致金屬氧化物半導(dǎo)體(MOS)管閾值電壓�����、跨導(dǎo)等性能參數(shù)退化�����,是集成電路失效的一個(gè)重要因素�����。本文通過(guò)物理建模的方法得到 HCI 失效的統(tǒng)計(jì)分布�����。
3.1.1物理模型
N 型金屬氧化物半導(dǎo)體(NMOS)器件 HCI 的壽命可用式(6)表示�����。
式中: W 為溝道寬度�����;DH 為有效擴(kuò)散系數(shù)�����; NitF 為器件失效時(shí)的界面陷阱密度,見(jiàn)式(7)�����; XH 為柵極厚度�����;Id 為漏端電流�����,見(jiàn)式 (8)�����; φit 為界面陷阱產(chǎn)生所需的最小能量�����,約為 3.7 eV�����; λ 為電子平均自由程�����,約為 7.8 nm�����;q 為電子電荷�����,為 1.6×10-19�����;Em為溝道中最大電場(chǎng)�����;K 為常數(shù),與界面處Si-H鍵的密度有關(guān)�����;B為常數(shù)�����。
式中:Esat為速度飽和電場(chǎng)(5×104 V/cm)�����;Leff為有效溝道長(zhǎng)度�����;Cox 為柵氧化物電容�����;ue為電子遷移率�����,其值受溫度T、柵電壓 Vg�����、閾值電壓 Vth及柵氧化物厚度 Tox 的影響,可用式(9)表示�����。
3.1.2 HCI失效分布的蒙特卡羅仿真
HCI 造成器件壽命離散的主要原因是光刻工藝的不均勻?qū)е聹系篱L(zhǎng)度不均�����,所以主要設(shè)定溝道有效長(zhǎng)度 Leff 為隨機(jī)參數(shù)�����,隨機(jī)變量符合正態(tài)分布。除此之外�����,還可將物理模型中的溫度T、漏源電壓Vds�����、柵電壓 Vg�����、 柵氧化物厚度 Tox、 柵極厚度 XH 等設(shè)置為隨機(jī)參數(shù)�����,以模擬集成電路在不同使用條件下的環(huán)境和器件狀態(tài)。本文以 130 nm 工藝為例�����,基于式(6)~式 (9)�����,對(duì)HCI的失效分布進(jìn)行蒙特卡羅仿真�����。
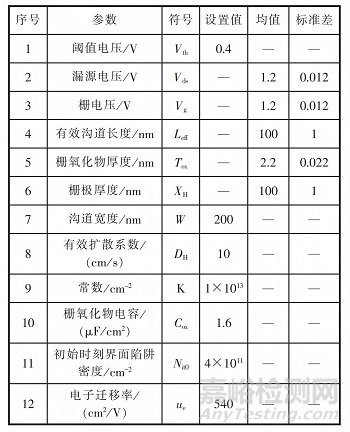
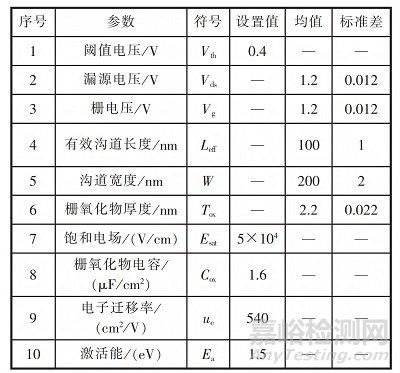
蒙特卡羅仿真所用器件的參數(shù)值如表1所示�����。
表1 蒙特卡羅仿真所用器件的參數(shù)值
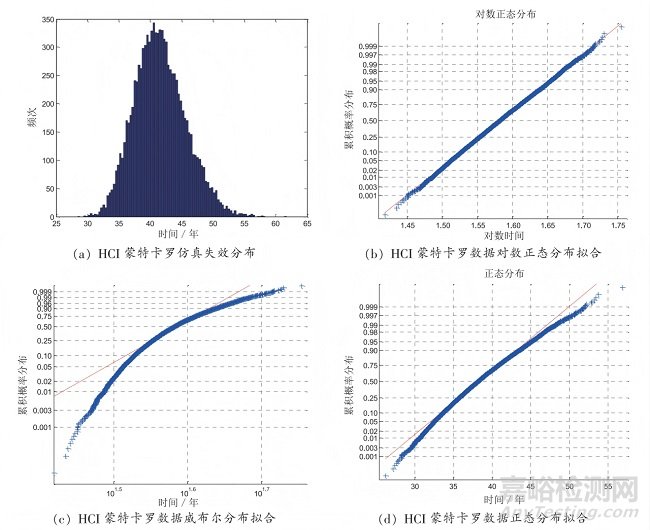
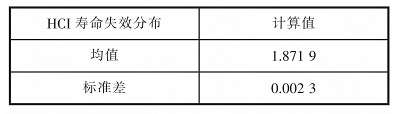
設(shè)定閾值電壓變化不小于10%為失效判據(jù),HCI蒙特卡羅仿真結(jié)果如圖1所示�����。從圖1可看出�����, 在對(duì)數(shù)正態(tài)坐標(biāo)系下, HCI 的失效分布趨于一條直線�����, 因此可確定 HCI 失效最符合對(duì)數(shù)正態(tài)分布�����。 HCI 失效分布計(jì)算結(jié)果如表2所示。
圖1 HCI 蒙特卡羅仿真結(jié)果
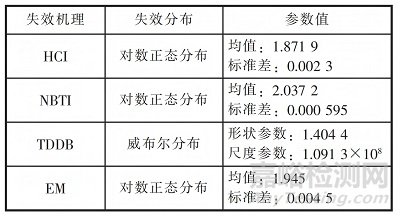
表2 HCI 失效分布計(jì)算結(jié)果
3.1.3 確定主要影響因素
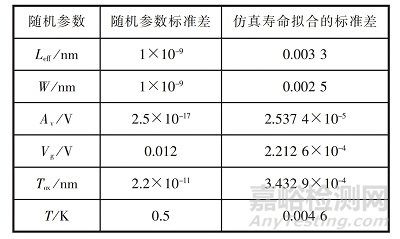
將表 1 中序號(hào)為2~6的隨機(jī)參數(shù)分別作為單一隨機(jī)變量進(jìn)行蒙特卡羅仿真�����,按式(2)和式 (3)計(jì)算失效分布的期望與方差�����,并根據(jù)式(4)和式(5) 反推得到仿真壽命的標(biāo)準(zhǔn)差,結(jié)果如表3所示。
表3 器件參數(shù)的離散值對(duì)壽命標(biāo)準(zhǔn)差的影響
從表 3 最后一列的計(jì)算結(jié)果可看出�����,有效溝道長(zhǎng)度、源漏電壓對(duì) HCI 壽命的離散度影響大�����,是NMOS 器件 HCI 壽命離散的主要影響因素�����。
3.2 NBTI
NBTI一般發(fā)生在P型金屬氧化物半導(dǎo)體(PMOS)器件中�����。在負(fù)柵壓及較高溫度作用下�����,器件發(fā)生退化�����,導(dǎo)致閾值電壓上升�����,遷移率�����、跨導(dǎo)�����、漏電流下降[5]�����。
3.2.1物理模型
假設(shè)初始界面陷阱造成的閾值電壓變化量ΔVth0 為0�����,靜態(tài)應(yīng)力下NBTI的壽命可用式(10)表示:
應(yīng)力過(guò)程中的閾值電壓變化量可用式(11)表示。
式中:δv 為除界面陷阱后其他氧化物電荷造成的閾值電壓變化量�����,近似為 5 mV�����; A 為常數(shù)�����,值為0.022�����;a 為常數(shù)�����,值為 4�����;E0 為電場(chǎng)強(qiáng)度�����,值為2.0 mV/cm�����;Ea 為溫度激活能�����,值為 0.13 eV�����。 其他參數(shù)可參考表1�����。
3.2.2 NBTI失效分布的蒙特卡羅仿真
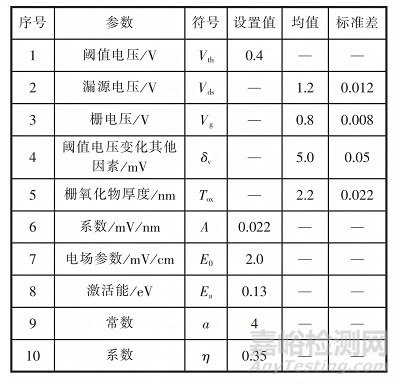
以130nm工藝為例�����,基于式(10)~式 (12)�����,對(duì) NBTI 的失效分布進(jìn)行蒙特卡羅仿真,仿真設(shè)定的器件參數(shù)值如表 4 所示�����。
表4 NBTI蒙特卡羅仿真設(shè)定的器件參數(shù)值
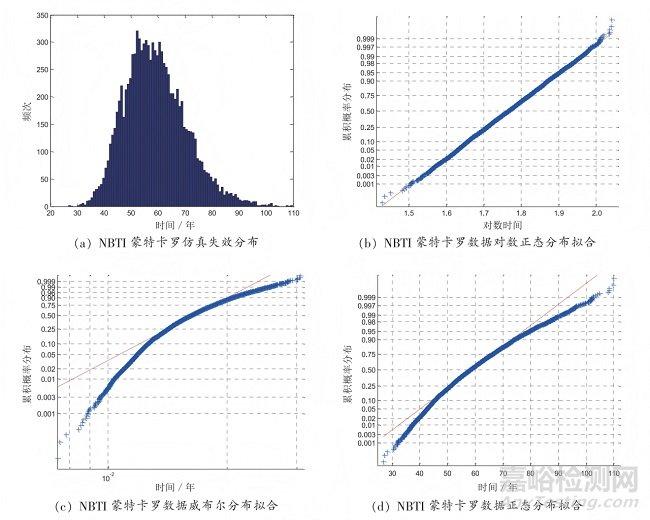
設(shè)定閾值電壓變化不小于10%為失效判據(jù)�����,蒙特卡羅仿真結(jié)果如圖 2 所示�����。
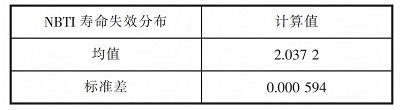
從圖 2 可看出�����,在對(duì)數(shù)正態(tài)坐標(biāo)系下�����,NBTI失效分布趨于一條直線�����,因此確定 NBTI 失效分布最符合對(duì)數(shù)正態(tài)分布�����。NBTI 失效分布計(jì)算結(jié)果如表 5 所示�����。
圖2 NBTI 蒙特卡羅仿真結(jié)果
表5 NBTI 失效分布計(jì)算結(jié)果
3.2.3 確定主要影響因素
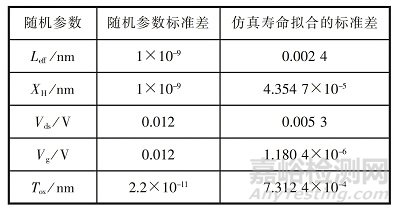
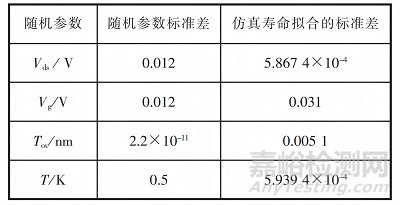
將表 4 中序號(hào)為 2~5 的隨機(jī)參數(shù)分別作為單一隨機(jī)變量進(jìn)行蒙特卡羅仿真�����,按式 (2) 和式 (3)計(jì)算失效分布的期望與方差�����,并根據(jù)式 (4) 和式 (5) 反推得到仿真壽命的標(biāo)準(zhǔn)差�����,結(jié)果如表 6 所示�����。從表 6 可看出�����,柵電壓對(duì)壽命的離散度影響最大,因此可確定柵電壓是 PMOS 器件NBTI壽命離散的主要影響因素�����。
表6 器件參數(shù)的離散值對(duì) NBTI 壽命標(biāo)準(zhǔn)差的影響
3.3 TDDB
TDDB是一種柵氧化層退化現(xiàn)象�����,一般認(rèn)為TDDB是由氧化層中缺陷累積而出現(xiàn)導(dǎo)電通路造成的�����。
3.3.1物理模型
TDDB 的失效符合威布爾分布�����。TDDB 累積失效函數(shù)可表示為式 (13) 所示的威布爾分布形式:
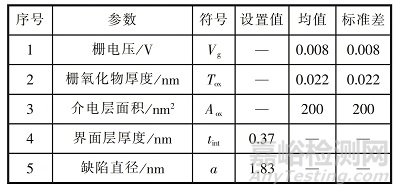
式中:Tox 為介電層厚度�����,tint 為界面層厚度�����, Aox 為介電層面積�����, a 為造成介電層導(dǎo)通缺陷的直徑�����,N(t)為 t 時(shí)刻介電層中的陷阱濃度�����。
由于陷阱濃度變化量和TDDB壽命呈反比�����,因此陷阱濃度可用 TDDB 的壽命模型反推�����。TDDB 退化模型符合冪率模型�����,則反推的陷阱濃度變化量可用式(14)表示�����。
式中:K為常數(shù);n 通過(guò)大量的實(shí)驗(yàn)室數(shù)據(jù)擬合得到�����,值為 44�����;Ea為激活能�����,值為 0.155 eV�����;k為玻爾茲曼常數(shù)�����;T 為溫度�����。
通過(guò)數(shù)學(xué)推導(dǎo)�����,威布爾分布的尺度參數(shù)可用式 (15)表示:
形狀參數(shù)可用式(16)表示�����。
TDDB 累積失效分布函數(shù)可用式(17)表示�����。
3.3.2 TDDB失效分布的蒙特卡羅仿真
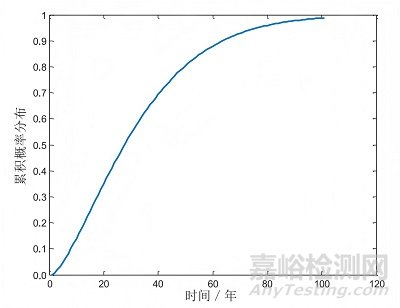
已知 TDDB 失效符合威布爾分布�����,因此蒙特卡羅仿真可求得威布爾分布的形狀參數(shù)和尺度參數(shù)�����,并由此得到概率累積分布�����。TDDB 蒙特卡羅仿真設(shè)置的器件參數(shù)值如表 7 所示�����。
表7 TDDB 蒙特卡羅仿真設(shè)定的器件參數(shù)值
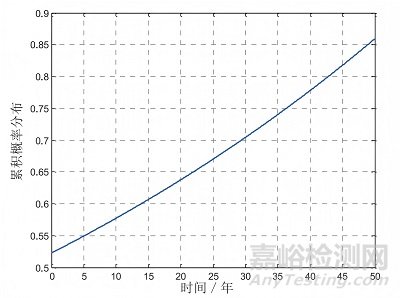
得到的仿真結(jié)果如圖 3 所示。
圖3 TDDB 累積分布
TDDB 失效分布計(jì)算結(jié)果如表8所示�����。
表8 TDDB 失效分布計(jì)算結(jié)果
改變參數(shù)設(shè)定值�����,仿真結(jié)果會(huì)得到不同的威布爾分布形狀參數(shù)和尺度參數(shù)�����。柵電壓�����、工作溫度對(duì)尺度參數(shù)有較大的影響�����。
3.4 EM
當(dāng)電流在導(dǎo)體中流動(dòng)時(shí)�����,大量電子的定向移動(dòng)將形成一種推力�����,不斷推動(dòng)著晶格原子向電流的反方向移動(dòng)�����。 在電流密度較大的區(qū)域�����, 晶格原子在“電子風(fēng)” 的沖刷下逐漸形成空洞�����; 而在電流密度較緩的區(qū)域�����, 原子又會(huì)逐漸堆積形成尖峰�����。 當(dāng)導(dǎo)體中的空洞不斷變大而使導(dǎo)體截?cái)啵?則會(huì)造成導(dǎo)線斷路�����; 尖峰所造成的應(yīng)力也將破壞微電子器件的結(jié)構(gòu), 從而導(dǎo)致其失效�����。
3.4.1 物理模型
EM 壽命模型如式(18) 所示�����。
式中:B 為常數(shù)�����,J 為電流密度�����,見(jiàn)式(19)�����。
式中:Av 為接觸孔面積�����,對(duì)于130nm工藝,為l×l04 nm2�����。 Id如式(8)所示�����,將其代入式 (19)�����,得到式(20)�����。
3.4.2 EM失效分布的蒙特卡羅仿真
以130nm工藝的NMOS觸點(diǎn)為例�����,基于式(18)~式(20)對(duì) EM 的失效分布進(jìn)行蒙特卡羅仿真�����。
EM失效蒙特卡羅仿真設(shè)定的器件參數(shù)值如表9 所示�����。
表9 EM蒙特卡羅仿真設(shè)定的器件參數(shù)值
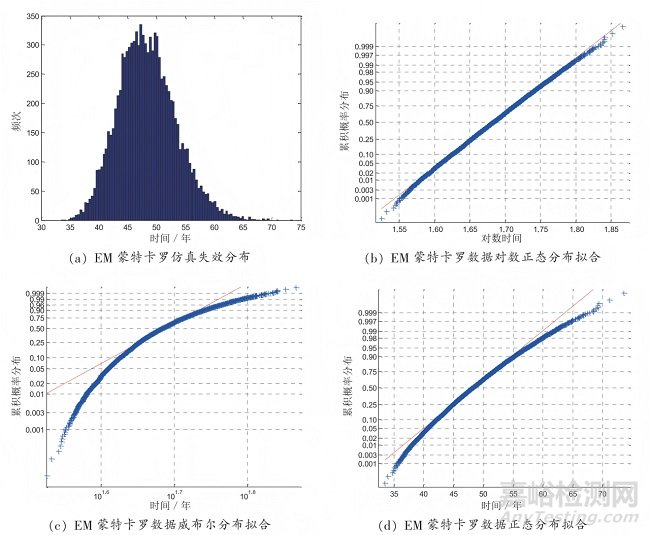
設(shè)定閾值電壓變化不小于10%為失效判據(jù)�����,仿真結(jié)果如圖 4 所示�����。通過(guò)圖 4 可看出�����,在對(duì)數(shù)正態(tài)坐標(biāo)系下�����,EM 失效分布趨于一條直線�����,因此確定 EM 失效符合對(duì)數(shù)正態(tài)分布�����。EM 失效分布計(jì)算結(jié)果如表 10 所示。
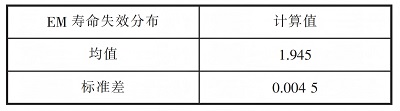
圖4 EM 蒙特卡羅仿真結(jié)果
表10 EM 失效分布計(jì)算結(jié)果
3.4.3 確定主要影響因素
將表 9 中序號(hào)為 2~6 的隨機(jī)參數(shù)分別作為單一隨機(jī)變量進(jìn)行蒙特卡羅仿真�����,按式(2)和式(3)計(jì)算失效分布的期望與方差�����,并根據(jù)式(4) 和式(5)反推得到仿真壽命的標(biāo)準(zhǔn)差�����,結(jié)果如表 11 所示�����。
表11 器件參數(shù)的離散值對(duì)壽命標(biāo)準(zhǔn)差的影響
從表11可看出�����,有效溝道長(zhǎng)度�����、溝道寬度和工作溫度對(duì)壽命的離散度影響大�����。因此�����,有效溝道長(zhǎng)度�����、溝道寬度和工作溫度是 NMOS 器件 EM 壽命離散的主要影響因素�����。
4 集成電路失效率的計(jì)算
上面討論了單個(gè) MOS 器件單一失效機(jī)理的失效分布�����。 MOS 器件是構(gòu)成集成電路的基本單元�����,一片集成電路中包含幾十到上百兆甚至更多數(shù)量的MOS 器件�����。 對(duì)于由多個(gè) MOS 管構(gòu)成的集成電路,在開(kāi)展失效率計(jì)算時(shí)�����, 在不考慮競(jìng)爭(zhēng)失效影響的前提下�����, 可假設(shè)任一 MOS 單管發(fā)生任一失效機(jī)理的失效都會(huì)造成集成電路的失效�����, 即假設(shè)所有的MOS 單管為串聯(lián)邏輯�����, 每個(gè)單管的失效機(jī)理也為串聯(lián)邏輯�����。 因此�����, 集成電路總失效率為所有MOS管的各失效機(jī)理失效率之和�����。
假設(shè)集成電路有 Mn 個(gè) NMOS 和 Mp 個(gè) PMOS�����,NMOS 與 PMOS 交替工作�����, 則每類 MOS 實(shí)際工作時(shí)間為總應(yīng)力時(shí)間的 1/2 �����。 集成電路的 4 種失效機(jī)理的失效分布函數(shù)可用式 (21) 表示�����。
假定集成電路中包含1000 個(gè) NMOS 和1000個(gè) PMOS�����,通過(guò)仿真進(jìn)行計(jì)算�����。集成電路仿真輸入?yún)?shù)如表 12 所示。
表12 集成電路仿真輸入?yún)?shù)
得到的集成電路總失效分布函數(shù)如圖5所示�����。根據(jù)失效分布函數(shù)可獲得集成電路的失效率預(yù)計(jì)�����。
圖5 集成電路總失效分布函數(shù)
5 精度分析
傳統(tǒng)可靠性預(yù)計(jì)方法需要大量的現(xiàn)場(chǎng)試驗(yàn)及故障數(shù)據(jù)�����, 其預(yù)計(jì)的準(zhǔn)確性依賴產(chǎn)品在實(shí)際應(yīng)用中積累的大量樣本數(shù)據(jù)及失效數(shù)據(jù)�����, 在試驗(yàn)或應(yīng)用不充分的情況下可靠性預(yù)計(jì)精度差�����。 由于現(xiàn)場(chǎng)數(shù)據(jù)并未區(qū)分是由于什么失效機(jī)理引起失效�����, 而是統(tǒng)一作為失效樣本進(jìn)行預(yù)計(jì)�����, 在每個(gè)產(chǎn)品的實(shí)際應(yīng)用中�����, 環(huán)境應(yīng)力的不同失效率應(yīng)有不同�����, 但在目前的工程中都使用同樣的失效率結(jié)果�����, 這將造成產(chǎn)品的過(guò)設(shè)計(jì)�����、 過(guò)保障現(xiàn)象�����。 隨著半導(dǎo)體技術(shù)的發(fā)展�����, 產(chǎn)品更新?lián)Q代越來(lái)越快, 傳統(tǒng)的預(yù)計(jì)方法還未能在手冊(cè)中提供失效率數(shù)據(jù)�����, 產(chǎn)品狀態(tài)就已經(jīng)發(fā)生變化�����, 這很難適應(yīng)半導(dǎo)體產(chǎn)品的快速發(fā)展�����。
基于失效物理的可靠性預(yù)計(jì)方法�����, 出發(fā)點(diǎn)是根據(jù)失效模式�����、 失效機(jī)理和失效位置來(lái)預(yù)測(cè)失效率�����,還能根據(jù)模型輸入?yún)?shù)的波動(dòng)確定輸出的分布特性�����, 進(jìn)而確定預(yù)計(jì)結(jié)果的置信度�����。 該方法考慮了環(huán)境條件�����、元器件材料�����、元器件質(zhì)量水平等因素對(duì)預(yù)計(jì)結(jié)果的影響�����, 提高了預(yù)計(jì)精度并擴(kuò)大了預(yù)計(jì)的范圍�����。 本文使用的蒙特卡羅仿真方法是在失效物理模型研究的基礎(chǔ)上�����, 對(duì)集成電路材料及質(zhì)量一致性水平等參數(shù)進(jìn)行了正態(tài)抽樣, 并通過(guò)合理地選取抽樣樣本大小保證了仿真結(jié)果誤差小于 0.01�����,仿真結(jié)果的置信度大于 0.998�����。 蒙特卡羅仿真結(jié)果的精度可根據(jù)需要進(jìn)行設(shè)定�����, 高的精度需要生成大的樣本�����,計(jì)算成本高�����。 在計(jì)算機(jī)能力迅猛發(fā)展的形勢(shì)下�����,以及狀態(tài)有界條件下�����, 計(jì)算能力已經(jīng)不是問(wèn)題�����,因此蒙特卡羅仿真方法可滿足工程不同精度的使用需求�����。
6 結(jié)束語(yǔ)
本文提出的方法應(yīng)用于 65 nm 制程的 SRAM存儲(chǔ)器�����, 將仿真得到的失效率預(yù)計(jì)結(jié)果和經(jīng) 1000 h加速試驗(yàn)得到的實(shí)測(cè)結(jié)果進(jìn)行比較�����, 發(fā)現(xiàn)準(zhǔn)確度均在86%以上�����, 證明了采用該方法進(jìn)行集成電路失效率預(yù)計(jì)的適用性�����。 本文以集成電路的理化分析為基礎(chǔ), 通過(guò)蒙特卡羅仿真方法得出集成電路單MOS 管各個(gè)失效機(jī)理的失效分布函數(shù)�����, 并將單管進(jìn)行串聯(lián)�����, 通過(guò)仿真獲得集成電路的失效分布函數(shù)�����, 從而可求得各個(gè)時(shí)間下的失效率�����, 開(kāi)拓了通過(guò)理化模型進(jìn)行集成電路可靠性預(yù)計(jì)的道路�����。
參考文獻(xiàn)
[1] 卞鳴鍇. 基于失效物理的集成電路失效率計(jì)算方法研究[D]. 廣州: 廣東工業(yè)大學(xué)�����, 2015.
[2] DAVID A H, HORACE G J�����, RESVE A S .Analysis and design of digital integrated circuits in deep submicron technology [M]. Mcgraw-hill companies, Inc�����, 2003: 334-336.
[3] KO P K�����,MULLER R S �����,HU C. A unified model for hot-electron currents in MOSFET's[C] //IEEE Proseedings of 1981. International elec-tron devices meeting. New York: IEEE�����, 1981:600-603.
[4] 彭建. 基于失效物理的電子系統(tǒng)可靠性預(yù)計(jì)研究與實(shí)現(xiàn)[D]. 成都: 電子科技大學(xué)�����, 2012.
[5] 韓慶田�����,劉夢(mèng)軍�����,賀孝濤�����,等. 可靠性預(yù)計(jì)及其發(fā)展趨向[J]. 電子產(chǎn)品可靠性與環(huán)境試驗(yàn)�����,2001 (5): 14-18.